






 |
 |
 |
 |
 |
 |
 |
Wie du vielleicht schon entdeckt hast, ist es legal, einer Variablen mehr als einmal einen Wert zuzuweisen. Eine neue Wertzuweisung bewirkt, dass eine schon existierende Variable nun auf einen neuen Wert verweist (und damit aufhört auf den früheren Wert zu verweisen).
bruce = 5
print bruce,
bruce = 7
print bruce
Die Ausgabe dieses Programms ist 5 7, weil das erste Mal, wenn bruce ausgegeben wird, ist der Wert dieser Variablen 5 und das zweite Mal ist ihr Wert 7. Das Komma am Ende der ersten print-Anweisung bewirkt, dass nach der Ausgabe des Strings keine neue Zeile begonnen wird. Deshalb erscheinen beide Ausgaben in einer Zeile.
Hier ist mehrfache Zuweisung in einem Zustandsdiagramm dargestellt:

Wenn man mit mehrfachen Zuweisungen arbeitet ist es besonders wichtig, zwischen Zuweisungsoperationen und Vergleichen zur Feststellung von Gleichheit zu unterscheiden. Weil Python das Gleichheitszeichen (=) für Zuweisungen verwendet, verfällt man leicht in den Fehler eine Anweisung wie a = b als einen Ausdruck für Gleichheit zu interpretieren. Das ist er aber nicht!
Zunächst ist Gleichheit kommutativ und Zuweisung nicht. Zum Beispiel gilt in der Mathematik, wenn a = 7 ist, dann ist auch 7 = a. Aber in Python ist die Anweisung a = 7 legal aber 7 = a ist (syntaktisch) nicht legal.
Außerdem ist in der Mathematik eine festgestellte Gleichheit immer wahr. Wenn jetzt a = b gilt, dann wird stets a gleich b sein. In Python kann eine Wertzuweisung zwei Variablen gleich machen, aber sie müssen deshalb nicht gleich bleiben:
a = 5
b = a # a and b are now equal
a = 3 # a and b are no longer equal
Die dritte Zeile ändert den Wert von a, aber sie ändert nicht den Wert von b, daher sind sie auch nicht mehr gleich. (In manchen Programmiersprachen wird ein anderes Symbol für die Wertzuweisung verwendet, wie z. B. <- oder :=, um diese Art von Verwechslung zu vermeiden.)
Obwohl mehrfache Wertzuweisungen häufig hilfreich sind, sollte man sie mit Vorsicht verwenden. Wenn die Werte von Variablen sich häufig ändern, kann das den Code schwer lesbar und schwer zu debuggen machen.
Computer werden oft verwendet, um immer wiederkehrende Aufgaben zu automatisieren. Die Wiederholung identischer oder ähnlicher Aufgaben ohne Fehler zu machen ist etwas, das Computer gut können, Menschen aber schlecht.
Wir haben zwei Programme gesehen, nLines() und countdown(), die Rekursion benützen um Wiederholungen auszuführen, was man auch Iteration nennt. Weil Iteration so häufig vorkommt, stellt Python mehrere Sprachelemente zur Verfügung, um ihre Verwendung zu erleichtern. Das erste davon, das wir jetzt betrachten werden, ist die while-Anweisung.
So schaut countdown() aus, wenn man eine while-Anweisung verwendet.
def countdown(n):
while n > 0:
print n
n = n-1
print "Blastoff!"
Da wir den rekursiven Aufruf entfernt haben, ist diese Funktion nicht rekursiv.
Denkt man sich für das englische Wort while das deutsche Wort "solange", so kann man die while-Anweisung beinahe so lesen, als wäre sie Umgangssprache. Sie bedeutet: "Solange n größer als 0 ist, fahre fort mit der Ausgabe von n auf den Bildschirm und anschließender Verminderung von n um 1. Wenn du bei 0 angekommen bist, dann gib das Wort "Blastoff!" aus.
Wir können das formaler darstellen als Programmablauf der while-Anweisung:
Der Körper besteht aus all den Anweisungen unter dem Kopf, die die gleiche Einrückungstiefe haben.
Dieser Typ von Programmablauf wird Schleife genannt, weil der dritte Schritt wieder zurück an den Anfang führt. Beachte, dass wenn die Bedingung schon bei der ersten Prüfung falsch ist, die Anweisungen im inneren der Schleife (im Schleifenkörper) niemals ausgeführt werden.
Der Körper der Schleife sollte den Wert von einer oder mehreren Variablen ändern, sodass schließlich die Bedingung falsch wird und die Schleife endet. Andernfalls wird die Schleife endlos wiederholt, was man naturgemäß eine Endlosschleife nennt.
An dieser Stelle enthält die englische Fassung dieses Kurses folgende Bemerkung:
An endless source of amusement for computer scientists is the observation that the directions on shampoo, "Lather, rinse, repeat," are an infinite loop.
Ob derart Treffendes auch auf deutsch beschrifteten Shampoo-Behältnissen steht, entzieht sich meiner Kenntnis. Bitte um Nachricht an den Übersetzer.
Im Falle von countdown(), können wir beweisen, dass die Schleife endet, weil wir wissen, dass der Wert von n endlich ist und wir können sehen, dass der Wert von n bei jedem Schleifendurchgang kleiner wird. Daher kommen wir schließlich bei 0 an. In anderen Fällen kann das nicht so leicht gesagt werden:
def sequence(n):
while n != 1:
print n,
if n%2 == 0: # n is even
n = n/2
else: # n is odd
n = n*3+1
Die Bedingung für diese Schleife ist n != 1, daher wird die Schleife solange ausgeführt, bis n gleich 1 ist, wodurch die Bedingung falsch wird.
Bei jedem Schleifendurchgang gibt das Progamm den Wert von n aus und prüft dann ob es gerade oder ungerade ist. Wenn er gerade ist wird der Wert von n durch 2 dividiert. Wenn er ungerade ist, wird der Wert ersetzt durch n*3+1. Wenn zum Beispiel der Startwert (das Argument, das der Funktion übergeben wird) 3 ist, dann ist die resultierende Zahlenfolge 3, 10, 5, 16, 8, 4, 2, 1.
Da n manchmal ansteigt und manchmal fällt, gibt es keinen offensichtlichen Beweis dafür, dass n jemals 1 erreichen wird oder dafür, dass das Programm jemals endet. Für einige spezielle Werte von n können wir beweisen, dass das Programm endet: z. B. wenn der Startwert eine Potenz von 2 ist, dann wird der Wert von n bei jedem Schleifendurchgang gerade bleiben, bis er schließlich 1 wird. Das vorangehende Beispiel endet mit einer solchen Folge, die mit 16 beginnt.
Abgesehen von speziellen Fällen ist es eine interessante Frage, ob wir beweisen können, dass dieses Programm für alle Werte von n endet. Bis heute ist niemand im Stande gewesen, das zu beweisen oder zu widerlegen.
Als eine Übung, schreibe die Funktion nLines() aus Abschnitt 4.9 neu, wobei du Iteration an Stelle von Rekursion benutzt.
Eines der Dinge, für die Schleifen gut sind, ist die Erzeugung von tabellarischen Daten. Bevor Computer so leicht verfügbar waren, mussten die Leute mit Logarithmen, Sinus- und Cosinuswerte mit der Hand rechnen. Um das zu erleichtern, enthielten Mathematikbücher lange Tabellen mit den Werten dieser Funktionen. Die Erzeugung dieser Tabellen war langsam und langweilig und sie hatten die Tendenz voller Fehler zu sein.
Als die Computer aufkamen, war eine der ersten Reaktionen: "Das ist großartig! Wir können die Computer benutzen, um diese Tabellen zu erzeugen. Dann werden keine Fehler mehr drin sein." Das stellte sich als (weitgehend) wahr aber kurzsichtig heraus. Denn bald danach waren Computer und Taschenrechner so allgegenwärtig, dass die Tabellen überflüssig wurden.
Gut, fast. Für manche Operationen benutzen Computer selbst Tabellen von Werten um näherungsweise Antworten zu erhalten und sie führen dann Rechnungen aus, um die Näherungswerte z verbessern. In manchen Fällen traten auch Fehler in den zugrundeliegenden Tabellen auf, am berühmtesten in der Tabelle, die der Intel Pentium benutzte um Gleitkomma-Divisionen durchzuführen.
Obwohl also eine "Logarithmen-Tafel" nicht mehr so nützlich ist, wie sie früher einmal war, ergibt sie doch ein gutes Beispiel für Iteration. Das folgende Programm gibt eine Folge von Werten in der linken Spalte aus und deren Logarithmen in der rechten Spalte:
x = 1.0
while x < 10.0:
print x, '\t', math.log(x)
x = x + 1.0
Der String '\t'+ stellt ein tab-Zeichen dar.
Wenn Zeichen und Strings auf dem Bildschirm dargetellt werden, kontrolliert eine unsichtbare Schreibmarke, der sogenannte Cursor, wo jeweils der nächste Buchstaben hingeschrieben wird. Nach einer print-Anweisung z. B. geht der Cursor normalerweise an den Anfang der nächsten Zeile.
Das tab-Zeichen verschiebt den Cursor nach rechts bis zum nächsten sogenannten tab-Stop. Tabs sind nützlich, um Spalten von Text gleichmäßig auszurichten, wie es die Ausgabe des vorstehenden Programms zeigt:
1.0 0.0
2.0 0.69314718056
3.0 1.09861228867
4.0 1.38629436112
5.0 1.60943791243
6.0 1.79175946923
7.0 1.94591014906
8.0 2.07944154168
9.0 2.19722457734
Wenn dir diese Werte merkwürdig vorkommen, denke daran, dass die log-Funktioin die Basis e benützt. Da Zweierpotenzen in der Computerwissenschaft so wichtig sind, wollen wir oft Logarithmen zur Basis 2 finden. Um das zu erreichen, können wir folgende Formel verwenden:
log2 x =
|
Andern wir die Ausgabe-Anweisung zu:
print x, '\t', math.log(x)/math.log(2.0)
so erhalten wir:
1.0 0.0
2.0 1.0
3.0 1.58496250072
4.0 2.0
5.0 2.32192809489
6.0 2.58496250072
7.0 2.80735492206
8.0 3.0
9.0 3.16992500144
Wir können sehen, dass 1, 2, 4 und 8 Zweierpotenzen sind, weil ihre Logarithmen zur Basis 2 ganze Zahlen sind. Wollen wir Logarithmen von anderen Potenzen von 2 finden, können wir das Programm wie folgt modifizieren:
x = 1.0
while x < 100.0:
print x, '\t', math.log(x)/math.log(2.0)
x = x * 2.0
Hier addieren wir nicht in jedem Schleifendurchgang etwas zu x, was eine arithmetische Folge erzeugt, sondern wir multiplizieren x jedesmal mit einem bestimmten Faktor, sodaß es eine geometrische Folge durchläuft. Das Ergebnis ist:
1.0 0.0
2.0 1.0
4.0 2.0
8.0 3.0
16.0 4.0
32.0 5.0
64.0 6.0
Wegen des tab-Zeichens zwischen den Spalten hängt die Poition der zweiten Spalte nicht von der Anzahl der Ziffern in der ersten Spalte ab.
Mögen Logarithmen-Tabellen auch nicht mehr besonders nützlich sein, so ist es für Computerwissenschaftler die Kenntnis der Potenzen von 2 sicherlich.
Als eine Übung ändere das Programm so ab, dass es die Potenzen von 2 bis hinauf zu 65 536 (das ist 216) ausgibt. Drucke sie aus und lerne sie auswendig.
Das backslash-Zeichen in '\t' zeigt den Anfang einer
escape-Sequenz an. Escape-Sequenzen gebraucht man, um
unsichtbare Zeichen wie tabs und Zeilenvorschub-Zeichen usw.
darzustellen. Die escape-Sequenz '\n' das newline-Zeichen
bewirkt, dass auf dem Bildschirm eine neue Zeile begonnen wird.
Eine escape-Sequenz kann überall in einem String auftreten; in dem Beispiel oben ist die tab-escape-Sequenz das einzige Ding in dem String.
Wie glaubst du wird man einen backslash in einem String darstellen?
Als eine Übung schreibe einen einzigen String, derdiese
Ausgabe
erzeugt.
Eine zweidimensionale Tabelle ist eine Tabelle, bei der man Werte an Schnittpunkten von Zeilen und Spalten abliest. Eine Multiplikationstafel ist ein gutes Beispiel. Angenommen du möchtest eine Multiplikationstafel für die Zahlen von 1 bis 6 erstellen.
Ein guter Ausgangspunkt ist es, eine Schleife zu schreiben, die die Vielfachen von 2 alle in eine Zeile schreibt:
i = 1
while i <= 6:
print 2*i, ' ',
i = i + 1
print
Die erst Zeile initialisiert eine Variable namens i, die als Zähler oder Zählvariable, auch Schleifenvariable fungiert. Wenn die Schleife ausgeführt wird, wird der Wert von i von 1 auf 6 erhöht. Wenn i 7 ist, endet die Schleife. Bei jedem Schleifendurchgang wird der Wert von 2*i, gefolgt von drei Leerzeichen ausgegeben.
Wiederum unterdrückt das Komma in der print-Anweisung dass eine neue Zeile begonnen wird. Nachdem die Schleife ferig ist, bewirkt die zweite print-Anweisung (nur), dass eine neue Zeile begonnen wird.
Die Ausgabe dieses Programms ist:
2 4 6 8 10 12
So weit, so gut. Der nächste Schritt ist, das was wir haben zu kapseln und zu verallgemeinern.
Der Prozeß der Kapselung besteht darin, ein Stück Code in eine Funktion zu verpacken und somit zu gestatten, alle die Vorteile, die Funktionen haben, zu nützen. Du hast bis jetzt zwei Beispiele von Kapselung gesehen: printParity() in Abschnitt ; und isDivisible() in Abschnitt 5.4.
Verallgemeinerung bedeutet, ausgehend von etwas Spezifischem - wie etwa: die Vielfachen von 2 auszugeben - etwas allgemeiner Verwendbares zu erzeugen, z. B. Ausgabe der Vielfachen einer beliebigen Zahl.
Die folgende Funktion kapselt die oben betrachtete Schleife und verallgemeinert sie so, dass Vielfachen von n ausgegeben werden.
def printMultiples(n):
i = 1
while i <= 6:
print n*i, '\t',
i = i + 1
print
Um zu kapseln, haten wir nur die erste Zeile hinzuzufügen, die den Namen der Funktion und die Parameterliste festlegt. Um zu verallgemeinern, mußten wir nur den Wert 2 durch den Parameter n ersetzen.
Wenn wir diese Funktion mit dem Argument 2 aufrufen, bekommen wir dieselbe Ausgabe wie vorher. Mit dem Argument 3 ist die Ausgabe:
3 6 9 12 15 18
Mit dem Argument 4, ist die Ausgabe:
4 8 12 16 20 24
Jetzt sind wir soweit, dass du wahrscheinlich schon erraten wirst,
wie man eine Multiplikationstabellen ausgeben kann nämlich
durch wiederholten Aufruf von printMultiples() mit verschiedenen
Argumenten. In der Tat können wir auch noch eine weitere Schleife
verwenden:
i = 1
while i <= 6:
printMultiples(i)
i = i + 1
Beachte, wie ähnlich diese Schleife zu der innerhalb von printMultiples() ist. Wir hatten nur die print-Anweisung durch einen Funktionsaufruf zu ersetzen.
Die Ausgabe dieses Programms ist eine Multiplikationstafel:
1 2 3 4 5 6
2 4 6 8 10 12
3 6 9 12 15 18
4 8 12 16 20 24
5 10 15 20 25 30
6 12 18 24 30 36
Um nocheinmal Kapselung vorzuzeigen, nehmen wir den Code vom Ende des Abschnitts 6.5 und verpacken auch ihn in eine Funktion:
def printMultTable():
i = 1
while i <= 6:
printMultiples(i)
i = i + 1
Dieser Prozess ist eine übliche Entwicklungs-Methode. Wir entwickeln Code, indem wir Codezeilen ausserhalb von Funktionen schreiben oder sie direkt in den interaktiven Interpreter schreiben. Sobald unser Code funktioniert, nehmen wir ihn heraus und verpacken ihn in eine Funktion.
Diese Vorgangsweise ist besonders nützlich, wenn du am Angfang der Entwicklung deines Programms noch nicht genau weißt, wie es in Funktionen aufgeteilt werden kann. Dieser Zugang gestattet dir, das Programm zu entwerfen, während du es entwickelst.
Vielleicht wundert es dich, wieso man dieselbe Variable, i, sowohl in printMultiples() als auch in printMultTable() verwenden kann. Verursacht es keine Probleme, wenn eine der Funktionen den Wert dieser Variablen verändert?
Die Antwort ist nein, denn das i in printMultiples() und das i in printMultTable() sind nicht dieselbe Variable.
Variablen, die innerhalb einer Funktionsdefinition erzeugt werden sind lokal; man kann eine lokale Variable nicht von ausserhalb der Funktion, in der sie erzeugt wurde, ansprechen. Das bedeutet, dass man die Freiheit hat mehrerer Variablen mit demselben Namen zu verwenden, solange das nicht in derselben Funktion geschieht.
Das Stack-Diagramm für dieses Programm zeigt, dass die zwei Variablen mit Namen i nicht dieselbe Variable sind. Sie können auf verschiedene Werte verweisen und eine Änderung von einer beinflusst nicht die andere.
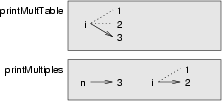
Der Wert von i in printMultTable() geht von 1 bis 6. In dem Diagramm ist er gerade 3. Beim nächsten Schleifendurchgang wird er 4 sein. Bei jedem Schleifendurchgang ruft printMultTable() die Funktion printMultiples() mit dem aktuellen Wert von i als Argument auf. Dieser Wert wird dem Parameter n zugewiesen.
Innerhalb von printMultiples() geht der Wert von i von 1 bis 6. Im Diagramm ist er gerade 2. Änderung dieser Variablen hat keine Auswirkung auf den Wert von i in printMultTable().
Es ist üblich und auch vollkommen legal, verschiedene lokale Variable mit demselben Namen zu verwenden. Insbesondere werden Namen wie i und j häufig für Schleifenvariable verwendet. Würdest du vermeiden, sie in einer Funktion zu verwenden, nur weil du sie auch schon anderswo verwendet hast, würde das wahrscheinlich dazu führen, dass das Programm schwerer lesbar wird.
Als ein weiteres Beispiel für Verallgemeinerung stelle dir nun vor, du hättest gerne eine Programm, das Multiplikationstabellen beliebiger Größe ausgeben könnte, nich nur die 6x6-Tabelle. Du könntest einen Parameter zu printMultTable() hinzufügen:
def printMultTable(high):
i = 1
while i <= high:
printMultiples(i)
i = i + 1
Wir haben den Wert 6 durch den Parameter high ersetzt. Wenn wir printMultTable() mit dem Argument 7 aufrufen, erhalten wir folgende Ausgabe:
1 2 3 4 5 6
2 4 6 8 10 12
3 6 9 12 15 18
4 8 12 16 20 24
5 10 15 20 25 30
6 12 18 24 30 36
7 14 21 28 35 42
Das ist fein, außer das wir vielleicht lieber hätten, das
die Tabelle quadratisch ist mit derselben Anzahl von Zeilen
und Spalten. Um das auch noch zu erreichen, fügen wir einen
weiteren Parameter zu printMultiples() hinzu um festzulegen,
wieviele Spalten die Tabelle haben soll.
Jetzt sind wir ein bißchen ekelhaft und nennen diesen Parameter wieder high, was zeigen soll, dass verschiedene Funktionen Parameter mit gleichem Namen haben können (gerade so wie lokale Variable). Hier ist das ganze Programm:
def printMultiples(n, high):
i = 1
while i <= high:
print n*i, '\t',
i = i + 1
print
def printMultTable(high):
i = 1
while i <= high:
printMultiples(i, high)
i = i + 1
Beachte: als wir einen neuen Parameter hinzugefügt haben, mussten wir die erste Zeile der Funktion (den Funktions-Kopf) ändern und auch die Stelle in printMultTable(), wo die Funktion aufgerufen wird.
Wie erwartet erzeugt dieses Programm eine quadratische 7x7-Tabelle:
1 2 3 4 5 6 7
2 4 6 8 10 12 14
3 6 9 12 15 18 21
4 8 12 16 20 24 28
5 10 15 20 25 30 35
6 12 18 24 30 36 42
7 14 21 28 35 42 49
Wenn du eine Funktion in geeigneter Weise verallgemeinerst, erhältst du oft ein Programm mit Fähigkeiten, die du gar nicht geplant hattest. Zum Beispiel könnte dir aufgefallen sein, dass, weil ab = ba, alle Einträge in der Tabelle zweimal vorkommen. Du könntest Tinte sparen, wenn du nur die Hälfte der Tabelle ausdruckst. Um das zu erreichen, musst du nur eine Zeile von printMultTable() ändern. Ändere
printMultiples(i, high)
zu
printMultiples(i, i)
und du erhältst
1
2 4
3 6 9
4 8 12 16
5 10 15 20 25
6 12 18 24 30 36
7 14 21 28 35 42 49
Als eine Übung verfolge die Ausführung dieser Version von printMultTable() und finde heraus, wie sie funktioniert.
Wir haben nun schon einige Male "all die Vorteile von Funktionen" erwähnt. Vielleicht fragst du dich immer noch, was denn all diese Vorteile sein sollen. Hier sind einige:
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
 |
 |
 |
 |
 |
 |
 |