






 |
 |
 |
 |
 |
 |
 |
Einige der eingebauten Funktionen, die wir benützt haben, wie z. B. die mathematischen Funktionen, haben Ergebnisse erzeugt. Der Aufruf solcher Funktionen erzeugt einen neuen Wert der an das aufrufende Programm "zurückgegeben" und dort normalerweise einer Variablen zugeordnet oder als Teil von einem Ausdruck verwendet wird.
e = math.exp(1.0)
height = radius * math.sin(angle)
Aber bis jetzt hat keine der Funktionen, die wir selbst geschrieben haben, einen Wert zurückgegeben.
In diesem Kapitel werden wir Funktionen schreiben, die Werte zurückgeben. Wir werden sie kurz Funktionen mit Wert nennen; wir suchen einen besseren Namen. Das erste Beispiel ist area(), das die Fläche eines Kreises mit gegebenem Radius zurückgibt.
import math
def area(radius):
temp = math.pi * radius**2
return temp
Wir haben die return-Anweisung schon früher gesehen, aber in einer Funktion mit Wert enthält die return-Anweisung einen Rückgabewert. Diese Anweisung bedeutet: "Kehre sofort von dieser Funktion zurück und benütze den folgenden Ausdruck als Rückgabewert." Der dafür vorgesehene Ausdruck kann beliebig kompliziert sein. Wir hätten daher auch obige Funktion in knapperer Form schreiben können:
def area(radius):
return math.pi * radius**2
Auf der anderen Seite erleichtern Hilfsvariablen wie temp das Auffinden von Fehlern.
Manchmal ist es nützlich, mehrere return-Anweisungen zu haben, eine in jedem Zweig einer bedingten Anweisung.
def absoluteValue(x):
if x < 0:
return -x
else:
return x
Da die return-Anweisungen in einer alternativen Verzweigung stehen, wird nur eine davon ausgeführt. Sobald eine ausgeführt ist, endet die Ausführung der Funktion, ohne dass irgendwelche folgenden Anweisungen ausgeführt werden.
Code, der nach einer return-Anweisung steht oder an irgendeiner anderen Stelle, die von der Programmausführung niemals erreicht werden kann, nennt man toten Code.
In einer Funktion mit Wert ist es eine gute Idee, sicherzustellen, dass jeder mögliche Weg durch das Programm schließlich auf eine return-Anweisung trifft.
def absoluteValue(x):
if x < 0:
return -x
elif x > 0:
return x
Dieses Programm ist nicht korrekt, weil wenn x zufällig gleich 0 ist, ist keine der beiden Bedingungen wahr und die Funktion endet ohne dass eine return-Anweisung ausgeführt wird. In diesem Fall wird ein spezieller Wert zurückgegeben: None.
>>> print absoluteValue(0)
None
Als Übung schreibe eine Funktion compare, die 1 zurückgibt, wenn x > y, 0 wenn x == y, und -1 wenn x < y ist.
An dieser Stelle solltest du imstande sein, den Code kompletter Funktionen zu lesen und zu verstehen, was er tut. Wenn du die Übungen ausgeführt hast, hast du auch schon einige kleine Funktionen geschrieben. Sobald du größere Funktionen schreibst, wirst du wahrscheinlich mehr Schwierigkeiten haben, speziell mit Laufzeitfehlern und logischen Fehlern.
Um mit zunehmend komplexeren Programmen umzugehen, möchten wir eine Technik empfehlen, die wir schrittweise Programmentwicklung nennen. Das Ziel der schrittweisen Programmentwicklung ist es, lange Sitzungen zur Fehlersuche zu vermeiden, indem wir unserem Programm Code jeweils nur in kleinen Abschnitten hinzufügen und testen.
Als Beispiel: angenommen, du möchtest die Entfernung zwischen zwei Punkten, die durch die Koordinaten (x1, y1) und (x2, y2) gegeben sind, finden. Nach dem pythagoräischen Lehrsatz ist diese Entfernung:
distance =
|
Der erste Schritt ist zu überlegen, wie eine distance-Funktion in Python ausschauen sollte. Mit anderen Worten, was sind die Eingaben (Parameter) und was ist die Ausgabe (Rückgabewert)?
In dieserm Fall sind die zwei Punkte die Eingabewerte, die wir darstellen können, indem wir vier Parameter benützen. Der Rückgabewert ist die Entfernung, die eine Gleitkommazahl sein wird.
Wir können nun schon eine Struktur für die Funktion aufschreiben:
def distance(x1, y1, x2, y2):
return 0.0
Offenbar berechnet diese Version der Funktion noch keine Entfernungen; sie gibt immer null zurück. Aber sie ist syntaktisch korrekt und sie ist lauffähig. Das heißt wir können sie testen, bevor wir sie weiterentwickeln.
Um die neue Funktoin zu testen, rufen wir sie mit Beispielwerten auf:
>>> distance(1, 2, 4, 6)
0.0
Wir haben die Werte so gewählt, dass die horizontale Entfernung 3 ist und die vertikale Entfernung 4; auf diese Weise sollte das Ergebnis 5 sein (die Hypotenuse eines 3-4-5 Dreiecks). Wenn man eine Funktion testet, ist es nützlich, die richtige Antwort zu wissen.
An diesem Punkt haben wir bestätigt, dass die Funktion syntaktisch
korrekt ist und wir können somit weitere Codezeilen hinzufügen. Nach
jedem Änderungsschritt werden wir die Funktion wieder testen. Wenn ein
Fehler an irgendeiner Stelle auftritt, wissen wir dann, wo er sein muss
in der letzten Zeile, die wir hinzugefügt haben.
Ein logischer erster Schritt in der Berechnung ist es, die Differenzen der Koordinaten x2 - x1 und y2 - y1 zu finden. Wir werden diese Werte in Hilfsvariablen mit den Namen dx und dy speichern und sie auf den Bildschirm ausgeben.
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
print "dx is", dx
print "dy is", dy
return 0.0
Wenn die Funktion richtig arbeitet, sollten die Ausgaben 3 und 4 sein, Ist das der Fall, wissen wir, dass die Funktion die richtigen Argumente erhält und die erste Berechnung richtig ausführt. Wenn nicht, dann sind nur wenige Zeilen zu überprüfen.
Als nächstes berechnen wir die Summe der Quadrate von dx und dy:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx**2 + dy**2
print "dsquared is: ", dsquared
return 0.0
Beachte, dass wir die print-Anweisungen, die wir im vorigen Schritt geschrieben haben, wieder entfernt haben. Solchen Code nennt man Gerüstcode, denn er ist hilfreich für die Konstruktion eines Programms aber nicht Teil der Endprodukts.
Wir lassen das Programm in dieser Entwicklungsstufe wieder laufen und überprüfen die Ausgabe (die hier 25 sein sollte).
Schließlich können wir, wenn wir den math-Modul importiert haben, die sqrt-Funktion verwenden um das Ergebnis zu berechnen und zurückzugeben.
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx**2 + dy**2
result = math.sqrt(dsquared)
return result
Wenn das richtig arbeitet, sind wir fertig. Andernfalls wirst du vielleicht den Wert von result vor der return-Anweisung auf den Bildschirm ausgeben wollen.
Wenn du beginnst zu programmieren, solltest du nur ein oder zwei Codezeilen auf einmal hinzufügen. Je mehr Erfahrung du gesammelt hast, desto eher wirst du größere Codeabschnitte schreiben, testen und debuggen. Jedenfalls kann dir die Methode der schrittweisen Programmentwicklung eine Menge Zeit für die Fehlersuche einsparen helfen.
Die wesentlichen Elemente dieser Vorgangsweise sind:
Als eine Übung verwende nun die Methode der schrittweisen Programmentwicklung um eine Funktion mit Namen hypotenuse zu schreiben, die die Länge der Hypotenuse eines rechtwinkeligen Dreiecks zurückgibt, wenn die Längen der zwei Katheten gegeben sind. (Notiere bei deiner Arbeit jede Entwicklungsstufe in dem schrittweisen Prozess).
Wie du wahrscheinlich schon erwartest, kann man eine Funktion von innerhalb einer anderen aufrufen. Diese Vorgangsweise nennt man Verknüpfung
Als Beispiel werden wir eine Funktion schreiben, die zwei Punkte, den Mittelpunkt eines Kreises und einen Punkt auf seinem Umfang als Parameter hat und die Fläche des Kreises berechnet.
Angenommen, dass der Mittelpunkt in den Variablen xc und yc gespeichert ist und der Punkt auf dem Umfang in den Variablen xp und yp. Der erste Schritt ist, den Radius des Kreises zu finden, d. h. den Abstand zwischen diesen beiden Punkten ist. Glücklicherweise gibt es eine Funktion distance(), die gerade das tut:
radius = distance(xc, yc, xp, yp)
Der zweite Schritt ist, die Fläche des Kreises mit diesem Radius zu finden und diesen Wert zurückzugeben:
result = area(radius)
return result
Wenn wir das in eine Funktion verpacken, erhalten wir:
def area2(xc, yc, xp, yp):
radius = distance(xc, yc, xp, yp)
result = area(radius)
return result
Wir haben diese Funktion area2() genannt, um sie von der area()-Funktion, die wir früher definiert haben zu unterscheiden. Es kann nur eine Funktion mit einem bestimmten Namen in einem gegebenen Modul geben.
Die Hilfsvariablen radius und result sind nützlich für die Entwicklung und die Fehlersuche, aber wenn das Programm einmal richtig funktioniert, könne wir es knapper gestalten, indem wir die Funktionsaufrufe verknüpfen:
def area2(xc, yc, xp, yp):
return area(distance(xc, yc, xp, yp))
Als eine Übung schreibe eine Funktion slope(x1, y1, x2, y2), die den Anstieg einer Geraden durch die Punkte (x1, y1) und (x2, y2) zurückgibt. Benütze dann diese Funktion in einer weiteren Funktion namens intercept(x1, y1, x2, y2), die für die Gerade durch die Punkte (x1, y1) und (x2, y2) den Anschnitt auf der y-Achse zurückgibt.
Funktionen können boolesche Werte zurückgeben, was oft bequem ist, wenn man komplizierte Überprüfungen in Funktionen verstecken möchte. Zum Beispiel:
def isDivisible(x, y):
if x % y == 0:
return 1 # it's true
else:
return 0 # it's false
Der Name dieser Funktion ist isDivisible(). Es ist gebräuchlich booleschen Funktioen Namen zu geben, die wie ja/nein - Fragen klingen. isDivisible gibt entweder 1 oder 0 zurück um anzuzeigen ob der Parameter x durch den Parameter y teilbar ist oder nicht.
Wir können die Funktion wieder kanpper formulieren, wenn wir vorteilhaft die Tatsache benützen, dass die Bedingung der if-Anweisung selbst ein boolescher Ausdruck ist. Wir können diesen direkt zurückgeben und damit die if-Anweisung ganz vermeiden:
def isDivisible(x, y):
return x % y == 0
Die folgende Sitzung zeift die neue Funktion in Aktion:
>>> isDivisible(6, 4)
0
>>> isDivisible(6, 3)
1
Boolesche Funktionen werden oft in bedingten Anweisungen verwendet:
if isDivisible(x, y):
print "x is divisible by y"
else:
print "x is not divisible by y"
Es mag verlockend sein, etwas wie das folgende zu schreiben:
if isDivisible(x, y) == 1:
...
Aber dieser Extra-Vergleich ist unnötig.
Als eine Übung schreibe eine Funktion isBetween(x, y, z), die 1 zurückgibt, wenn y < x < z oder 0 andernfalls.
Bis jetzt hast du erst eine kleine Teilmenge von Python gelernt, aber es wird dich vielleicht interessieren zu efahren, dass diese Teilmenge eine vollständige Programmiersprache ist. Das bedeutet, dass alles, was überhaupt berechnet werden kann in dieser Sprache ausgedrückt werden kann. Jedes Programm, das jemals geschrieben wurde, könnte auch ausschließlich mit den Sprachelementen formuliert werden, die du bis jetzt gelernt hast (genau genommen würdest du noch ein paar Befehle brauchen, um Geräte wie die Tastatur, die Maus, Disks usw. anzusprechen, aber das ist alles).
Diese Behauptung zu beweisen ist eine nicht triviale Übung, die zuerst Alan Turing gelungen ist, einem der ersten Computerwissenschafter (manche würde behaupten, dass er ein Mathematiker war, aber viele frühe Computerwissenschafter begannen als Mathematiker). Dementsprechend wird sie als Turing-These bezeichnet. Wenn du dich mit theoretischer Informatik beschäftigst, wird dir der Beweis wahrscheinlich über den Weg laufen.
Um dir eine Vorstellung davon zu geben, was du mit den Werkzeugen, die du bis jetzt gelernt hast, anstellen kannst, werden wir uns mit ein paar rekursiv definierten mathematischen Funktionen beschäftigen. Eine rekursive Definition ist in dem Sinn einer zirkulären Definition ähnlich, als die Definition einen Bezug auf die Sache enthält, die definiert wird. Eine echt zirkuläre Definition ist nicht sehr nützlich:
Würdest du diese Definition in einem Wörterbuch finden, wärest du wohl verärgert. Wenn du andererseits die Defnition der mathematischen Funktion Faktorielle nachschaust, wirst du ungefähr folgendes finden:
|
0! = 1 n! = n · (n-1)! |
Diese Definition besagt, dass die Faktorielle von 0 gleich 1 ist und dass die Faktorielle von jedem anderen Wert, n, gleich n multipliziert mit der Faktoriellen von n-1 ist. So ist 3! gleich 3 mal 2!, und das ist gleich 2 mal 1!, und das ist gleich 1 mal 0!. Setzt man das alles zusammen, so wird 3! gleich 3 mal 2 mal 1 mal 1 und das ergibt 6.
Wenn du eine rekursive Definition von etwas aufschreiben kannst, dann kannst du normalerweise auch ein Python-Programm schreiben, um das auszurechnen. Der erste Schritt ist zu entscheiden, was die Parameter für diese Funktion sind. Mit nur geringer Anstrengung solltest du zu dem Schluß kommen, dass die Faktorielle, also die Funktion factorial(), nur einen einzigen Parameter hat:
def factorial(n):
Sollte das Argument 0 sein, so brauchen wir nur 1 zurückgeben:
def factorial(n):
if n == 0:
return 1
Andernfalls, und das ist der interessantere Teil, müssen wir einen rekursiven Aufruf machen um die Faktorielle von n-1 zu finden und dann diese mit n multiplizieren:
def factorial(n):
if n == 0:
return 1
else:
recurse = factorial(n-1)
result = n * recurse
return result
Der Progammablauf für dieses Programm ist ähnlich wie der Ablauf von countdown() in Abschnitt 4.9. Wenn wir factorial() mit dem Wert 3 aufrufen, schaut er so aus:
Da 3 nicht gleich 0 ist, nehmen wir den zweiten Zweig und berechnen die Faktorielle von 3-1...
Da 2 nicht gleich 0 ist, nehmen wir den zweiten Zweig und berechnen die Faktorielle von 2-1...
Da 1 nicht gleich 0 ist, nehmen wir den zweiten Zweig und berechnen die Faktorielle von 1-1...
Da 0 gleich 0 ist, nehmen wir den ersten Zweig und geben 1 zurück ohne weitere rekursive Aufrufe zu machen.Der Rückgabewert (1) wird multipliziert mit n, welches hier 1 ist, und das Ergebnis, 1, wird zurückgegeben.
Der Rückgabewert (1) wird multipliziert mit n, welches hier 2 ist, und das Ergebnis, 2, wird zurückgegeben.
Der Rückgabewert (2) wird multipliziert mit n, welches hier 3 ist, und das Ergebnis, 6, wird zurückgegeben als der Rückgabewert des Funktionsaufrufes, der den ganzen Prozess ins Rollen gebracht hat.
Und so schaut das Stackdiagramm für diese Folge von Funktionsaufrufen aus:
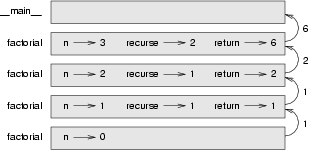
Dabei ist auch eingezeichnet, wie die Rückgabewerte den Stack hinaufgereicht werden. In jedem Rahmen ist der Rückgabewert der Wert von result, welches das Produkt von n und recurse ist.
Beachte, dass im letzten Stackelement die lokalen Variablen recurse und result nicht existieren, weil der Zweig, der sie erzeugt nicht ausgeführt wurde.
Den Programmablauf zu verfolgen ist ein Weg um Programme zu lesen, aber der kann schnell ziemlich mühsam werden. Eine Alternative ist das, was wir hier "Vertrauensvorschuß" nennen. Wenn du zu zu einem Funktionsaufruf kommst, dann vertraue darauf (anstatt dem Programmablauf zu folgen), dass die Funktion korrekt funktioniert und den passenden Wert zurückgibt.
In der Tat brigst du ja schon dieses Vertrauen auf, wenn du eingabaute Funktionen verwendest. Wenn du math.cos() oder math.exp() aufrufst, überprüfst du ja auch nicht die Implementationen dieser Funktionen. Du nimmst einfach an, dass sie richtig funktionieren, weil die Leute, die diese eingebauten Funktionsbibliotheken geschrieben haben, gute Programmierer sind.
Dasselbe trifft auch zu, wenn du eine deiner eigenen Funktionen
aufrufst. Wir haben zum Beispiel im Abschnitt 5.4, eine
Funktion mit dem Namen isDivisible() geschrieben, die herausfindet,
ob eine Zahl durch eine andere teilbar ist. Haben wir uns einmal überzeugt,
dass diese Funktion korrekt ist durch Testen und Überprüfung des
Codes können wir diese Funktion benützen ohne jedesmal wieder den
Code anzuschauen.
Dasselbe trifft auch auf rekursive Programme zu. Wenn du zum rekursiven Aufruf kommst, solltest du (anstatt dem Programmablauf zu folgen) annehmen, dass der rekuresive Aufruf richtig arbeitet (d. h. das korrekte Ergebnis liefert) und dich dann fragen: "Angenommen, ich kann die Faktorielle von n-1 finden, kann ich dann die Faktorielle von n berechnen?" In diesem Fall ist es klar, dass das geht, nämlich durch Multiplikation mit n.
Natürlich ist es ein bißchen seltsam, anzunehmen, dass die Funktion korrekt arbeitet, wenn du sie noch nicht einmal fertig programmiert hast, und darum sagen wir hier dass du mit einem Vertrauensvorschuß arbeitest.
Im vorhergehenden Beispiel haben wie Hilfsvariable benutzt, um die Schritte genau hinzuschreiben und den Code so zu gestalten, dass wir Fehler leicht finden können. Aber wir hätten auch einige Zeilen einsparen können:
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
Von jetzt an werden wir hier eher die knappere Form benützen, aber wir raten dir, eher die ausführlichere Form zu benützen, solange du Programmcode entwickelst. Wenn er einmal richtig arbeitet, kannst du ihn ja immer noch knapper gestalten, wenn du dazu Lust verspürst.
Nach der Faktoriellen ist das bekannteste Beispiel für eine rekursiv definierte mathematische Funktion fibonacci(). Fibonacci hat die folgende Definition:
|
fibonacci(0) = 1 fibonacci(1) = 1 fibonacci(n) = fibonacci(n-1) + fibonacci(n-2); |
In Python übersetzt schaut das so aus:
def fibonacci (n):
if n == 0 or n == 1:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
Wenn du versuchst, hier dem Programmablauf zu folgen, wird dir dein Kopf schon für ziemlich kleine Werte von n platzen. Aber entsprechend unserer Methode des Vertrauensvorschusses ist es klar, dass du, unter der Annahme dass die beiden rekursiven Aufrufe richtig funktionieren, das richtige Ergebnis erhältst, wenn du ihre beiden Rückgabewerte addierst.
Was geschieht, wenn wir factorial() mit dem Argument 1.5 aufrufen?
>>> factorial (1.5)
RuntimeError: Maximum recursion depth exceeded
Schaut nach unendlicher Rekursion aus. Aber wie kann das sein? Es gibt
doch einen Basis-Fall wenn n == 0. Das Problem ist hier, dass
die Werte von n den Basis-Fall verfehlen.
Im ersten rekursiven Aufruf ist der Wert von n gleich 0.5. Im nächsten ist er -0.5. Von da weg wird er immer kleiner und kleiner, aber er wird niemals gleich 0.
Wir haben hier zwei Möglichkeiten zur Auswahl. Wir können versuchen, die factorial()-Funktion zu verallgemeinern, damit sie auch mit Gleitkommazahlen funktioniert; oder wir können factorial() dazu bringen, den Typ des übergebenen Arguments zu überprüfen. Die erste Option führt zur sogenannten Gamma-Funktion und ist ein bißchen außerhalb des Rahmens dieser Ausführungen. So wählen wir die zweite Option:
Wir können type() verwenden um den Typ des Parameters mit dem Typ einer bekannten ganzen Zahl (z. B. 1) zu vergleichen. Wenn wir schon dabei sind, stellen wir auch gleich sicher, dass der Parameter nicht negativ ist:
def factorial (n):
if type(n) != type(1):
print "Factorial is only defined for integers."
return -1
elif n < 0:
print "Factorial is only defined for positive integers."
return -1
elif n == 0:
return 1
else:
return n * factorial(n-1)
Nun haben wir drei Basis-Fälle. Der erste fängt nicht ganzzahlige Argumente ab, der zweite negative ganze Zahlen. In beiden Fällen gibt das Programm eine Fehlermeldung auf den Bildschirm aus und einen speziellen Wert, -1, zurück um anzuzeigen, dass irgendetwas falsch gelaufen ist.
>>> factorial ("fred")
Factorial is only defined for integers.
-1
>>> factorial (-2)
Factorial is only defined for positive integers.
-1
Wenn wir einmal weiter als bis zu diesen beiden Überprüfungen gekommen sind, dann wissen wir, dass n eine positive ganze Zahl ist und wir können zeigen, dass die Rekursion einmal abbricht.
Dieses Programm demonstriert ein Muster, dass manchmal als Wächter bezeichnet wird. Die ersten beiden Zweige spielen die Rolle von Wächtern, die den nachfolgenden Code vor Werten bewahren, die einen Fehler verursachen könnten. Die Wächter ermöglichen zu beweisen, dass der Code korrekt ist.
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
 |
 |
 |
 |
 |
 |
 |