






 |
 |
 |
 |
 |
 |
 |
Rohübersetzung -- bitte um Rückmeldungen über Fehler und Unklarheiten an Mike Müller
Bäume bestehen genauso wie verkettete Listen aus Knoten. Ein gebräuchlicher Baum ist ein binärer Baum, in dem jeder Knoten einen Verweis auf zwei andere Knoten hat, die auch null sein können. Die Verweise werden als linker und und rechter Unterbaum bezeichnet. Wie verkettete Listen enthalten auch Bäume Inhalte. Ein Zustandsdiagramm für einen Baum sieht so aus:
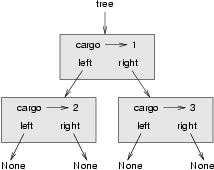
Um das Bild nicht zu überfrachten, werden mit None bezeichneten Knoten oft weggelassen.
Der oberste Teil des Baumes, hier mit dem Knoten baum bezeichnet, wird die Wurzel genannt. Um das sprachliche Bild konsistent zu halten, werden die andern Knoten Äste genannten. Die Knoten an den Spitzen mit den Null-Verweisen werden Blätter genannt. Es mag seltsam erscheinen, dass wir das Bild mit der Wurzel oben und den Blättern unten zeichnen, aber das ist noch nicht das Merkwürdigste.
Um die Sache noch zu verkomplizieren, nutzen Informatiker
gleichzeitig noch ein weiteres Bild den Familienbaum. Der
oberste Knoten wird manchmal Elternknoten genannten und die
Knoten auf die er verweist werden als seine Kinder
bezeichnet. Knoten mit dem gleichen Elternknoten heißen dann Geschwister
Schließlich werden geometrische Ausdrücke für die Beschreibung von Bäumen genutzt. Link und rechts wurden schon erwähnt. Es gibt auch die Begriffe "nach oben" (in Richtung des Elternknoten/ der Wurzel) und "nach unten" (in Richtung Kinder/Blätter). Weiterhin stehen alle Knoten, die die gleiche Entfernung zur Wurzel haben auf einer Höhenstufe des Baums.
Um sich über Bäume auszutauschen benötigt man wahrscheinlich nicht drei sprachlicher Bilder, aber es gibt sie nun einmal.
So wie verkettete Listen sind Bäume rekursive Datenstrukturen, weil sie rekursiv definiert sind.
Ein Baum ist entweder:
- der leere Baum, repräsentiert durch None oder
- ein Knoten, der einen Objektverweis und und zwei Baumverweise enthält.
Das Zusammenstellen eines Baumes ähnelt dem Zusammenstellen einer verketteten Liste. Jeder Aufruf des Konstruktors erstellt einen einzelnen Knoten.
class Baum:
def __init__(self, inhalt, links=None, rechts=None):
self.inhalt = inhalt
self.links = links
self.rechts = rechts
def __str__(self):
return str(self.inhalt)
Der inhalt kann einen beliebigen Typ haben, aber die Parameter links und rechts sollten Bäume sein. links und rechts sind optional; der Vorgabewert is None.
Um einen Knoten auszudrucken, drucken wir einfach seinen Inhalt.
Wir können den Baum von unten nach oben aufbauen. Zuerst werden die Kindknoten zugewiesen:
links = Baum(2)
rechts = Baum(3)
Danach wird der Elternknoten erstellt und mit den Kinder verbunden:
baum = Baum(1, links, rechts);
Wir können diesen Code prägnanter schreiben, indem wir die Konstruktoraufrufe schachteln:
>>> baum = Baum(1, Baum(2), Baum(3))
Egal welchen Weg wir wählen, das Ergebnis ist immer der Baum, wie er am Anfang des Kapitels beschrieben wurde.
Jedesmal wenn du eine neue Datenstruktur siehst sollte deine erste Frage lauten "Wie durchlaufe ich sie?". Der natürlichste Weg einen Baum zu durchlaufen, ist rekursiv. Wenn der Baum zum Beispiel Ganzzahlen als Inhalt enthält, gibt diese Funktion deren Summe zurück:
def gesamt(baum):
if baum == None: return 0
return gesamt(baum.links) + gesamt(baum.rechts) + baum.inhalt
Der Basisfall ist der leere Baum, der keinen Inhalt enthält und deshalb eine Summe von 0 hat. Der rekursive Schritt macht zwei rekursive Funktionsaufrufe, um die Summe der Kindbäume zu finden. Nach dem die rekursiven Aufrufen beendet sind, addieren wir den Inhalt des Elternknoten hinzu und geben die Gesamtsumme zurück.
Ein Baum stellt eine natürliche Art dar, die Struktur eines Ausdrucks abzubilden. Im Gegensatz zu anderen Notationen, kann er die Rechnung eindeutig darstellen. So ist zum Beispiel der Ausdruck 1 +2 * 3 in Infix-Notation mehrdeutig, es sei denn wir wissen, dass die Multiplikation Vorrang for der Addition hat.
Dieser Ausdrucksbaum bildet die gleiche Rechnung ab:
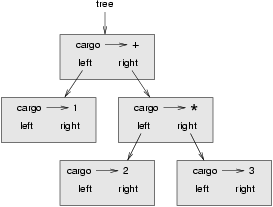
Die Knoten eines Audrucksbaumns können Operanden wie 1 und 2 oder Operatoren wie + und * sein. Operanden sind Blattknoten. Operatoren enthalten Verweise zu ihren Operanden. (Alle diese Operatoren sind binär, haben also genau zwei Operanden.)
Wir können diesen Baum so aufbauen:
>>> baum = Baum('+', Baum(1), Baum('*', Baum(2), Baum(3)))
Wenn man sich die Abbildung ansieht, gibt es keine Frage wie die Reihenfolge der Operationen ist; die Multiplikation wird zuerst ausgeführt, um den zweiten Operanden für die Addition zu berechnen.
Ausdrucksbäume haben viele Anwendungsmöglichkeiten. Das Beispiel in diesen Kapitel nutzt Bäume, um Ausdrücke in Postfix-, Prefix- und Infix-Notation zu übersetzen. Ähnliche Bäume werden in Kompilern verwendet, um Programme zu parsen, zu optimieren und zu übersetzen.
Wir können einen Ausdrucksbaum durchlaufen und seinen Inhalt folgendermaßen drucken:
def druckeBaum(baum):
if baum == None: return
print baum.inhalt,
druckeBaum(baum.links)
druckeBaum(baum.rechts)
Anders ausgedrückt wird um einen Baum zudrucken der Inhalt der Wurzel gedruckt, danach wird der gesamte linke Unterbaum gedruckt, gefolgt vom rechten Unterbaum. Diese Art des Druckens eines Baumes wird als Vor-Reihenfolge bezeichnet, da der Inhalt der Wurzel vor dem Inhalt der Kinder gedruckt wird. Für das vorangegangene Beispiel wäre der Output folgender:
>>> baum = Baum('+', Baum(1), Baum('*', Baum(2), Baum(3)))
>>> druckeBaum(baum)
+ 1 * 2 3
Dieses Format unterscheidet sich sowohl von der Postfix- als auch der Infix-Notation. Es handelt sich um eine weitere Notation, in der die Operatoren vor den Operanden erscheinen, die Prefix-Notation genannt wird.
Man könnte nun schlussfolgern, dass bei einem Durchlaufen des Baumes in in einer anderen Reihenfolge der Ausdruck in einer anderen Notation erscheint. Wenn man zum Beispiel die Unterbäume zuerst und dann den Wurzelknoten druckt, erhält man:
def druckeBaumInNachReihenfolge(baum):
if baum == None: return
druckeBaumInNachReihenfolge((baum.links)
druckeBaumInNachReihenfolge((baum.rechts)
print baum.inhalt,
Das Ergebnis, 1 2 3 * +, erscheint in Postfix-Notation. Diese Reihenfolge des Durchlaufens wird als Nach-Reihenfolge bezeichnet.
Schließlich kann man einen Baum in Zwischen-Reihenfolge ausdrucken, indem zuerst der linke Baum, dann die Wurzel und dann der rechte Baum gedruckt wird:
def druckeBaumInZwischenReihenfolge(baum):
if baum == None: return
druckeBaumInZwischenReihenfolge(baum.links)
print baum.inhalt,
druckeBaumInZwischenReihenfolge(tree.rechts)
Das Ergebnis ist 1 + 2 * 3, also ein Ausdruck in Infix-Notation.
Um fair zu sein, müssen wir zugeben, dass wir eine bedeutende Erschwernis ausgelassen haben. Manchmal wenn wir einen Ausdruck in Infix-Notation schreiben, müssen wir Klammern verwenden, um die Reihenfolge der Operationen zu erhalten. Deshalb ist ein Durchlaufen mit Zwischen-Reihenfolge nicht ganz ausreichend, um einen Ausdruck in Infix-Notation zu erhalten.
Wie dem auch sei, mit ein paar Verbesserungen bieten der Ausdrucksbaum und die drei Arten des rekursiven Durchlaufens einen allgemeinen Weg Ausdrücke von einem Format ins andere zu übersetzen.
Modifiziere die Methode druckeBaumInZwischenReihenfolge als Übung so, dass sie Klammern um jeden Operator und jedes Operandenpaar setzt. Ist der Output richtig und eindeutig? Sind die Klammern immer nötig?
Wenn wir den Baum mit Zwischen-Reihenfolge durchlaufen und nachverfolgen auf welcher Höhenstufe des Baumes wir sind, können wir eine grafische Darstellung des Baums erzeugen:
def druckeBaumEingerueckt(baum, hoehenstufe=0):
if baum == None: return
druckeBaumEingerueckt(baum.rechts, hoehenstufe+1)
print ' '*hoehenstufe + str(baum.inhalt)
druckeBaumEingerueckt(baum.links, hoehenstufe+1)
Der Parameter hoehenstufe behält die Übersicht darüber, wo wir uns im Baum befinden. Anfangs ist dessen Wert standardmäßig 0. Jedesmal wenn wir einen rekursiven Aufruf machen, übergeben wir hoehestufe+1, da die Höhenstufe des Kindes eins größer ist als die des Elternknoten. Jedes Element wird um zwei Leerzeichen pro Höhenstufe eingerückt. Das Ergebnis für den Beispielbaum sieht so aus:
>>> druckeBaumEingerueckt(baum)
3
*
2
+
1
Wenn du dir den Ausdruck seitwärts ansiehst, siehst du eine vereinfachte Version der ursprünglichen Darstellung.
In diesem Abschnitt parsen wir Ausdrücke in Infix-Notation und bauen draus den dazugehörigen Ausdrucksbaum. So ergibt zum Beispiel der Ausdruck (3+7)*9 den folgenden Baum:
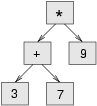
Bitte beachte, dass wir das Diagramm vereinfacht haben, indem wir die Namen der Attribute weggelassen haben.
Der Parser, den wir schreiben werden, kann Ausdrücke, die Zahlen, Klammern und die Operatoren + und * enthalten bearbeiten. Wir setzen voraus, dass der Eingangsstring bereits in eine Python-List, also in Token umgewandelt wurde. Die Token-Liste für (3+7)*9 ist:
['(', 3, '+', 7, ')', '*', 9, 'end']
Das Token end ist dafür nützlich, den Parser davon abzuhalten über das Ende der Liste hinaus zu lesen.
Als Übung, schreibe eine Funktion, die einen Ausdruck als String entgegen nimmt und eine Liste mit Token zurückgibt.
Als erste Funktion schreiben wir gibToken, die eine Liste von Token und einen erwarteten Token als Parameter übernimmt. Sie vergleicht den erwarteten Token mit dem ersten Token in der Liste: wenn sie übereinstimmen, entfernt sie den ersten Token der Liste und gibt wahr zurück; andernfalls gibt sie falsch zurück:
def gibToken(tokenListe, erwartet):
if tokenListe[0] == erwartet:
del tokenListe[0]
return 1
else:
return 0
Da sich tokenListe auf ein veränderbares Objekt bezieht, werden die Veränderungen für jede andere Variable sichtbar, die sich auf das gleiche Objekt bezieht.
Die nächste Funktion gibZahl behandelt die Operanden. Wenn das nächste Token in tokenListe eine Zahl ist, entfernt gibZahl diesen gibt einen Blattknoten zurück, der die Zahl enthält; andernfalls gibt es None zurück.
def gibZahl(tokenListe):
x = tokenListe[0]
if type(x) != type(0): return None
del tokenListe[0]
return Baum (x, None, None)
Bevor wir weiter machen sollten wir gibZahl für sich testen. Wir weisen tokenListe eine Liste mit Zahlen zu, entnehmen die erste, drucken das Ergebnis und drucken was von der Tokenliste übrig bleibt:
>>> tokenListe = [9, 11, 'end']
>>> x = gibZahl(tokenListe)
>>> druckeBauminNachReihenfolge(x)
9
>>> print tokenListe
[11, 'end']
Die nächste Methode, die wir brauchen, ist gibProdukt, die einen Ausdrucksbaum von Produkten aufbaut. Ein einfaches Produkt hat zwei Zahlen als Operanden, wie 3 * 7
Hier ist dieser Version von gibProdukt, die einfache Produkte behandelt.
def gibProduct(tokenListe):
a = gibZahl(tokenListe)
if gibToken(tokenListe, '*'):
b = gibZahl(tokenListe)
return Baum ('*', a, b)
else:
return a
Wenn wir annehmen, das gibZahl erfolgreich ist und einen Baum als Singelton zurückgibt, können wir den ersten Operator a zuweisen. Wenn das nächste Zeichen ein * ist, bekommen wir die zweite Zahl und bauen einen Ausdrucksbaum, mit a und b und dem Operator auf.
Falls das nächste Zeichen ein anderes ist, geben wir einfach den Blattknoten mit a zurück. Hier sind zwei Beispiele:
>>> tokenListe = [9, '*', 11, 'end']
>>> baum = gibProdukt(tokenListe)
>>> druckeBauminNachReihenfolge(baum)
9 11 *
>>> tokenListe = [9, '+', 11, 'end']
>>> baum = gibProdukt(tokenListe)
>>> druckeBauminNachReihenfolge(baum)
9
Das zweite Beispiel besagt, dass wir einen einzelnen Operanden als eine Art Produkt betrachten. Diese Definition von "Produkt" ist nicht intuitiv, erweist aber sich als nützlich.
Nun müssen wir uns mit zusammengesetzten Produkten wie 3 * 5
* 13. Wir behandeln diesen Ausdruck als Produkt von Produkten,
nämlich 3 * (5 * 13). Der resultierende Baum sieht so aus:
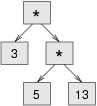
Mit einer kleinen Änderung in gibProdukt können wir beliebig lange Produkte bearbeiten:
def gibProdukt(tokenListe):
a = gibZahl(tokenListe)
if gibToken(tokenListe, '*'):
b = gibProdukt(tokenListe) # diese Zeile wurde geaendert
return Baum ('*', a, b)
else:
return a
Mit anderen Worten, ein Produkt kann entweder ein Singelton oder ein Baum mit * an der Wurzel, einer Zahl links und einem Produkt rechts sein. Diese Art von rekursiver Definition sollte dir langsam bekannt vorkommen.
Testen wir die neue Version mit einem zusammengesetzten Produkt:
>>> tokenListe = [2, '*', 3, '*', 5 , '*', 7, 'end']
>>> baum = gibProdukt(tokenListe)
>>> druckeBauminNachReihenfolge(baum)
2 3 5 7 * * *
Als Nächstes werden wir die Fähigkeit Summen zu parsen hinzufügen. Wiederum nutzen wir eine nicht sehr intuitive Definition für Summe. Für uns kann eine Summe ein Baum mit + an der Wurzel, einem Produkt auf der linken und einer Summe auf der rechten Seite sein. Eine Summe kann auch einfach ein Produkt sein.
Wenn du dich auf ein Spiel mit dieser Definition einlässt, wirst du ein schöne Eigenschaft entdecken: wir können jeden beliebigen Ausdruck (ohne Klammern) als Summe von Produkten ausdrücken. Diese Eigenschaft ist die Grundlage für unseren Pars-Algorithmus.
Die Funktion gibSumme versucht einen Baum mit einem Produkt auf der linken und einer Summe auf der rechten Seite aufzubauen. Wenn es aber kein + findet, versucht sie einfach ein Produkt zu bilden.
def gibSumme(tokenListe):
a = gibProdukt(tokenListe)
if gibToken(tokenListe, '+'):
b = gibSumme(tokenListe)
return Baum ('+', a, b)
else:
return a
Testen wir diese Funktion mit 9 * 11 + 5 * 7:
>>> tokenListe = [9, '*', 11, '+', 5, '*', 7, 'end']
>>> baum = gibSumme(tokenListe)
>>> druckeBauminNachReihenfolge(baum)
9 11 * 5 7 * +
Wir sind fast fertig, müssen aber noch Klammern behandeln. An einer beliebigen Stelle im Ausdruck, wo eine Zahl sein kann, kann auch eine gesamte Summe stehen, die in Klammern eingeschlossen ist. Wir müssen nur gibZahl modifizieren, um Unterausdrücke zu behandeln:
def gibZahl(tokenListe):
if gibToken(tokenListe, '('):
x = gibSumme(tokenListe) # den Unterausdruck abholen
gibToken(tokenListe, ')') # schliessende Klammern entfernen
return x
else:
x = tokenList[0]
if type(x) != type(0): return None
tokenList[0:1] = []
return Tree (x, None, None)
Test wir dies mit 9 * (11 + 5) * 7:
>>> tokenListe = [9, '*', '(', 11, '+', 5, ')', '*', 7, 'end']
>>> tree = gibSumme(tokenListe)
>>> druckeBauminNachReihenfolge(baum)
9 11 5 + 7 * *
Der Parser hat die Klammern richtig behandelt; die Addition erfolgt vor der Multiplikation.
In der Endversion des Programms wäre es eine gute Idee gibZahl einen neuen Namen zu geben, der seine neue Rolle besser beschreibt.
Im gesamten Parser haben wir angenommen, dass Ausdrücke wohlgeformt sind. So nehmen wir zum Beispiel an, dass das nächste Zeichen nach dem Ende des Unterausdrucks eine schließende Klammer ist. Wenn aber nun eine Fehler auftritt und das folgende Zeichen keine schließende Klammer ist, sollten wir diesen abfangen.
def gibZahl(tokenListe):
if gibToken(tokenListe, '('):
x = gibSumme(tokenListe)
if not gibToken(tokenListe, ')'):
raise 'FalscherAusdruckFehler', 'fehlende Klammern'
return x
else:
# Rest der Funktion wurde weggelassen
Die Anweisung raise wirft eine Ausnahme; in diesem Fall werfen wir eine neue Art von Ausnahme, die wir FalscherAusdruckFehler nennen. Wenn die Funktion, die gibZahl oder eine andere Funktion im Traceback (eng. Zurückverfolgung) gerufen hat, die Ausnahme behandelt, kann das Programm weiter ausgeführt werden. Andernfalls druckt Python eine Fehlermeldung und beendet sich.
Als Übung, finde andere Stellen in diesen Funktionen, wo Fehler auftreten können und füge geeignete raise-Anweisungen ein. Teste dein Programm mit falsch geformten Ausdrücken.
In diesem Abschnitt entwickeln wir ein kleines Programm, das einen Baum verwendet um eine Wissensdatenbank abzubilden.
Das Program interagiert mit dem Anwender, um einen Baum mit Fragen und Tiernamen aufzubauen. Hier ist Beispielsprogrammlauf:
Denkst du an ein Tier? j
Ist es ein Tier "Vogel"? n
Wie ist der Name des Tieres? Hund
Welche Frage wuerde das Tier "Hund" vom Tier "Vogel" unterscheiden? Kann es fliegen
Wenn das Tier ein Tier "Hund" waere, waere die Antwort? n
Denkst du an ein Tier? j
Kann es fliegen? n
Ist es ein Tier "Hund"? n
Wie ist der Name des Tieres? Katze
Welche Frage wuerde das Tier "Katze" vom Tier "Hund" unterscheiden? Bellt
es
Denkst du an ein Tier? j
Kann es fliegen? n
Bellt es? y
Ist es ein Tier "Hund"? y
Ich habe gewonnen!
Denkst du an ein Tier? n
Hier ist der Baum, den dieser Dialog aufbaut:
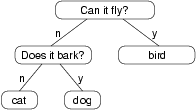
Am Beginn jeder Spielrunde beginnt das Programm an der Spitze des Baumes und stellt die erste Frage. In Abhängigkeit von der Antwort bewegt es sich zum linken oder rechten Kindknoten und fährt fort, bis es zu einem Blattknoten kommt. An dieser Stelle trifft es eine Annahme. Wenn die Annahme nicht richtig ist, fragt es den Anwender nach dem Namen des Tieres und nach einer Frage, die die falsche Annahme vom neuen Tier unterscheidet. Dann fügt es den Knoten mit der neuen Frage und dem neuen Tier zum Baum hinzu:
Hier ist der Code:
def tier():
# beginne mit einem Singelton
wurzel = Baum('Vogel')
# Schleife, bis Anwender beendet
while 1:
print
if not yes('Denkst du an ein Tier? '): break
# den Baum durchlaufen
baum = wurzel
while baum.gibLinken() != None:
eingabeaufforderung = baum.gibInhalt() + "? "
if ja(eingabeaufforderung):
baum = baum.gibRechten()
else:
baum = baum.gibLinken()
# Annahme treffen
annahme = baum.gibInhalt()
eingabeaufforderung = 'Ist es ein ' + annahme + '? "
if ja(eingabeaufforderung):
print "Ich habe gewonnen!"
continue
# neue Informationen holen
eingabeaufforderung = 'Wie ist der Name des Tieres? '
tier = raw_input(eingabeaufforderung)
eingabeaufforderung = 'Welche Frage wuerde das Tier "%s" vom Tier "%s" unterscheiden?'
fragen = raw_input(eingabeaufforderung % (tier,annahme))
# neue Informationen zum Baum hinzufuegen
baum.setzeInhalt(frage)
eingabeaufforderung = 'Wenn das Tier ein Tier "%s" waere, waere die Antwort? '
if ja(eingabeaufforderung % tier):
bum.setzeLinken(Baum(annahme))
baum.setzeRehten(Baum(tier))
else:
baum.setzeLinken(Baum(tier))
baum.setzeRechten(Baum(annahme))
Die Funktion ja is ein Helfer. Sie druckt eine Eingabeaufforderung und nimmt dann die Eingabe vom Anwender. Wenn die Antwort mit j oder J beginnt, gibt die Funktion wahr zurück:
def ja(frage):
from string import lower
antwort = lower(raw_input(frage))
return (antwort[0] == 'j')
Die Bedingung für die äußere Schleife ist 1, was bedeutet das Programm fährt fort, bis die breack-Anweisung ausgeführt wird und der Anwender nicht an ein Tier denkt.
Die innere while-Schleife durchläuft den Baum von oben nach unten, geleitet von den Reaktionen des Anwenders.
Wenn ein neuer Knoten zum Baum hinzugefügt wird, ersetzt die neue Frage den Inhalt und die beiden Kinder sind das neue Tier und den originalen Inhalt.
Ein Nachteil des Programms besteht darin, dass nach dem Beenden alles vergisst, was du ihm so sorgfältig beigebracht hast!
Als Übung, denke dir mehrere Wege aus, mit denen den Wissensbaum in einer Datei speichern kannst. Implementiere die Lösung von der du glaubst, dass sie die einfachste ist.
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
 |
 |
 |
 |
 |
 |
 |