Kapitel 19

Rohübersetzung -- bitte um Rückmeldungen über Fehler und Unklarheiten an Mike Müller

Queues

Diese Kapitel behandelt zwei ADT: die Queue und die Prioritätsqueue. In realen Leben ist eine Queue (eng. Warteschlange, [kju:]) eine Schlange von Kunden, die eine Dienstleistung warten. In den meisten Fällen, ist der erste Kunde in der Schlange auch der erste der bedient wird. Natürlich gibt es auch Ausnahmen. So werden an Flughäfen Kunden, deren Flug bald geht auch aus der Mitte der Schlange nach vorn gerufen. Im Supermarkt lässt ein höflicher Kunden jemanden mit nur wenigen eingekauften Stücken vor.

Die Regel, die bestimmt wer als nächstes dran ist wird als Queueing Policy bezeichnet. Die einfachste Queueing Policy nennt man FIFO, das beutet "first-in-first-out" (eng. für zuerst rein zuerst raus). Die allgemeinste Queueing Policy ist die Prioritätsqueue, bei der jedem Kunden eine Priorität zugewiesen wird, wobei der Kunde mit der höchsten Priorität zuerst drankommt, unabhängig von der Anstellreihenfolge. Wir nennen das die allgemeinste Policy, weil die Priorität durch beliebige Kriterien bestimmt werden kann: zu welcher Uhrzeit ein Flug geht; wie viele Lebensmittel ein Kunden im Wagen hat; oder auch wie bedeutend der Kunde ist. Natürlich sind nicht alle Queueing Policies "fair", aber Fairness ist subjektiv.

Der ADT Queue und der ADT Prioritätsqueue haben die gleiche Menge Operationen. Die Differenz besteht in der Semantik der Operationen: eine Queue nutzt die FIFO-Policy, während die Prioritätsqueue (wie der Name andeutet) queueing nach der Priorität nutzt.

19.1 The Queue ADT

Der ADT Queue wird durch folgende Operationen definiert:

__init__

Initialisierung einer neuen. leeren Queue.

einfuegen

Füge ein neues Element zu der Queue hinzu.

entfernen

Entferne ein Element von der Queue gibt es Ergebnis zurück. Das Element, das zurückgegeben wird, ist das zuerst hinzugefügte.

istLeer

Kontrolliere ob die Queue leer ist.

19.2 Verkettet Queue

Die erste Implementierung des ADT Queue sieht so aus wie sie heißt, verkette Queue, da sie aus verketten Knoten-Objekten besteht. Die Klassendefinition sieht so aus:

class Queue:
  def __init__(self):
    self.laenge = 0
    self.kopf = None

  def istLeer(self):
    return (self.leange == 0)

  def einfuegen(self, inhalt):
    knoten = Knoten(inhalt)
    knoten.naechster = None
    if self.kopf == None:
      # Wenn die Liste leer kommt der neue Knoten zuerst.
      self.kopf = knoten
    else:
      # Finde den letzten Knoten in der Liste.
      letzter = self.kopf
      while letzter.naechster: letzter = letzter.naechster
      # Hänge den neuen Knoten an.
      letzter.naechster = knoten
    self.laenge = self.laenge + 1

  def entfernen(self):
    inhalt = self.kopf.inhalt
    self.kopf = self.kopf.naechster
    self.laenge = self.laenge - 1
    return inhalt

Die Methoden istLeer entsprcht der gleichnamigen in dem ADT Stack und entfernen ist analog zu entferneZweiten in der Klasse VerketteteListe. Die Methode einfuegen ist neue und etwas komplizierter.

Wir möchten neue Elemente am End e der Liste hinzufügen. Wenn die Queue leer ist, lassen wir einfach kopf auf den neue Knoten zeigen. Andernfalls gehen wird durch die Liste bis zum letzten Knoten und hängen den neuen Knoten am Ende an. Wir können den letzten Knoten darin erkenne, dass sein Attribut naechster None ist.

Ein ordentlich aufgebautes Objekt Queue hat zwei Unveränderliche. Der Wert von laenge soll der Anzahl der Knoten in der Queue entsprechen. Weiterhin sollte das Attribut naechster des letzten Knotens den Wert None besitzen. Überzeuge dich davon, dass dies Methode beide Unveränderliche im richtigen Zustand erhält.

19.3 Leistungscharakteristiken

Wenn wir eine Methode rufen kümmern wir uns normaler Weise nicht um die Details er Implementierung. Aber es gibt ein "Detail", das wir kennen sollten     die Leistungscharakteristiken der Methode. Wie lange dauert es und wie ändert sich die Laufzeit, wen die Anzahl der Element in der Sammlung steigt?

Sehen wir uns zuerst entfernen an. Es gibt keine Schleifen oder Funktionsaufrufe, so dass man davon ausgehen kann, dass die die Laufzeit der Methode jedes mal die gleiche ist. Eine solche Methode wird zeitkonstante Methode genannt. In der Realität wird die Methode ein klein wenig schneller sein, wenn die Liste leer ist, da es den Inhalt der Bedingungsabfrage überspringt. Der Unterschied ist aber nicht significant.

Die Leistung von von einfuegen ist da ganz anders. Im allgemeinen Fall müssen wird die Liste durchlaufen, um das letzte Element zu finden.

Diese Durchlaufen der Liste beansprucht Zeit, die der Länge der Liste Proportional ist. Da die Laufzeit eine linearen Funktion der Länge ist, wird diese Methode als zeitlich linear bezeichnet. Verglichen mit linearer Zeit ist das sehr schlecht.

19.4 Verbesserte verkettete Queue

Wir hätten gern eine Implementierung des ADT Queue, die alle Operationen in konstanter Zeit ausführen kann. Ein Weg dies zu erreichen ist die Klasse Queue so zu modifizieren, dass sie eine Referenz sowohl zum ersten als auch zum letzten Knoten aufrechterhält, so wie in der Abbildung dargestellt:

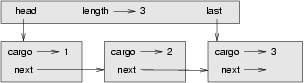
Die Implementierung der Klasse VerbesserteQueue sieht nun so aus:

class VerbesserteQueue:
  def __init__(self):
    self.laenge = 0
    self.kopf  = None
    self.letzter   = None

  def istLeer(self):
    return (self.laenge == 0)

Bis hierhin besteht die einzige Änderung das Attribut letzter. Es wird in den Methoden einfuegen und entfernen verwendet:

class VerbesserteQueue:
  ...
  def einfuegen(self, inhalt):
    knoten = Knoten(inhalt)
    knoten.naechster = None
    if self.laenge == 0:
      # Wenn die Liste leer ist, ist der neue Knoten kopf und letzter
      self.kopf = self.letzter = knoten
    else:
      # Finde den letzten Knoten.
      letzter = self.letzter
      # Haenge den neuen Knoten an.
      letzter.naechster = knoten
      self.letzter = knoten
    self.laenge = self.laenge + 1

Da wir mit letzter den letzten Knoten referenzieren, müssen wir nicht mehr suchen. Als Ergebnis ist diese Methode zeitkonstant.

Es ist allerdings ein Preis für diese Geschwindigkeit zu zahlen. Wir müssen einen Spezialfall in entfernen einführen, um letzter auf None zu setzten, wenn der letzte Knoten entfernt wird: There is a price to pay for that speed. We have to add a special case to remove to set last to None when the last node is removed:

class VerbesserteQueue:
  ...
  def entfernen(self):
    inhalt = self.kopf.inhalt
    self.kopf = self.kopf.naechster
    self.laenge = self.laenge - 1
    if self.laenge == 0:
      self.letzter = None
    return inhalt

Diese Implementierung ist komplizierter als die der verketten Queue und es ist deshalb auch schwieriger zu zeigen, dass sie korrekt ist. Der Vorteil besteht darin, dass wir unser Ziel erreicht haben     sowohl einfuegen als auch entfernen ins zeitkonstante Operationen.

Als eine Übung, schreibe eine Implementierung des ADT Queue unter Verwendung einer Python-Liste. Vergleiche die Leistung dieser Implementierung mit der von VerbesseretQueue für unterschiedliche Längen der Queue.

19.5 Prioritätsqueue

Der ADT Prioritätsqueue hat das gleiche Interface wie der ADT Queue aber eine unterschiedliche Semantik. Hier nochmal das Interface:

__init__

Initialisiere eine neu Queue.

einfuegen

Fuege ein neues Element zur Queue hinzu.

entfernen

Ein Element aus der Queue entfernen und zurückgeben. Das zurückgegebene Element ist das mit der höchsten Priorität.

istLeer

Kontrolliere, ob die Queue leer ist.

Der Unterschied in der Semantik liegt, dass von der Queue entfernte Element nicht notwendiger Weise das zuerst hinzugefügte Element ist. Stattdessen ist es das Element, das die höchste Priorität hat. Was die Prioritäten sind und wie sie miteinander verglichen werden, wird durch die Implementierung der Prioritätsqueue nicht spezifiziert. Es hängt davon ab welche Elemente in der Queue sind.

So könnte zum Beispiel eine alphabetische Reihenfolge gewählt werden, wenn die Elemente in der Queue Namen sind. Wenn es sich um Bowling-Ergebnisse handelt, wäre eine Reihenfolge vom höchsten zum niedrigsten Ergebnis sinnvoll. Wenn es dagegen Golf-Ergebnisse sind wäre es eher die umgekehrte Reihenfolge. So lange wir die Element in der Queue vergleichen können, könne wir auch das Element mit der höchsten Priorität finden und entfernen.

Diese Implementierung der Prioritätsqueue hat als Attribut eine Pythonliste, die die Elemente der Queue enthält.

class PrioritaetsQueue:
  def __init__(self):
    self.items = []

  def istLeer(self):
    return self.items == []

  def einfuegen(self, item):
    self.items.append(item)

Die Intialisierungsmethode und die Methoden istLeer und einfuegen sind alle Furniere von Listenoperationen. Die einzige interessante Methode ist entfernen:

class PrioritaetsQueue:
  ...
  def entfernen(self):
    maxi = 0
    for i in range(1,len(self.items)):
      if self.items[i] > self.items[maxi]:
        maxi = i
    item = self.items[maxi]
    self.items[maxi:maxi+1] = []
    return item

Am Anfang jeder Iteration wird in maxi der Index des größten Elements (mit der höchsten Priorität) gespeichert, das bisher betrachte wurde. Bei jedem Schleifendurchlauf vergleicht das Programm das i-te Element mit dem Spitzenreiter. Wenn das neue Element größer ist, wird der Wert von maxi auf i gesetzt.

Nachdem das die for-Schliefe vollständig durchlaufen ist, ist maxi der Index des größten Elements. Dieses Element wird entfernt und als Ergebnis zurückgegeben.

Testen wir die Implementierung:

>>> q = PrioritaetsQueue()
>>> q.einfuegen(11)
>>> q.einfuegen(12)
>>> q.einfuegen(14)
>>> q.einfuegen(13)
>>> while not q.istLeer(): print q.entfernen()
14 13 12 11

Wenn die Queue einfache Zahlen oder Strings enthält, werden diese in numerischer oder alphabetischer Reihenfolge entfernt, immer vom höchsten zum niedrigsten. Python kann die größte Zahl oder den größten String finden, da es diese mit den eingebauten Vergleichsoperatoren vergleichen kann.

Wenn die Queue einen Objekttyp enthält, muss sie eine Methode __cmp__ bereitstellen. Wenn die Methode entfernen den Operator > für eien Vergleich nutzt, ruft es die Methode __cmp__ für eins der Elemente auf und übergibt das anders als Parameter. So lange die Methode __cmp__ richtig funktioniert funktioniert auch die PriorotätsQueue.

19.6 Die Klasse Golfer

Als Beispiel für ein Objekt mit einer ungewöhnlichen Definition der Priorität implementieren wir eine Klasse namens Golfer, die den Überblick über die Namen und Spielergebnisse der Golfer behält.Wie gewöhnlich starten wir mir der Definition von __init__ und __str__:

class Golfer:
  def __init__(self, name, ergebnis):
    self.name = name
    self.ergebnis= ergebnis

  def __str__(self):
    return "%-16s: %d" % (self.name, self.ergebnis)

Die Methode __str__ nutzt den Formatoperator, um Namen und Spielergebnisse in ordentliche Spalten zu schreiben.

Als nächstes definieren wir eine Version von __cmp__ , dei der das niedrigste Ergebnis die höchste Priorität bekommt. Wie immer gibt __cmp__ 1 als Ergebnis zurück, wenn self "größer " als other ist und -1 wenn self "kleiner als" other ist oder 0 wenn sie gleich groß sind.

class Golfer:
  ...
  def __cmp__(self, other):
    if self.score < other.score: return  1   # less is more
    if self.score > other.score: return -1
    return 0

Jetzt sind wir bereit die Prioritätsqueue mit der Klasse Golfer zu testen:

>>> tiger = Golfer("Tiger Woods",    61)
>>> phil  = Golfer("Phil Mickelson", 72)
>>> hal   = Golfer("Hal Sutton",     69)
>>>
>>> pq = PrioritaetsQueue()
>>> pq.einfuegen(tiger)
>>> pq.einfuegen(phil)
>>> pq.einfuegen(hal)
>>> while not pq.istLeer(): print pq.entfernen()
Tiger Woods    : 61 Hal Sutton     : 69 Phil Mickelson : 72

als eine Übung, schreibe eine Implementierung des ADT Prioritätsqueue unter Verwendung einer verketteten Liste. Du solltest die Liste immer sortiert halten, so das das Entfernen eine Operation mit konstanter Zeit ist. Vergleiche die Leistung dieser Implementierung mit der der Implementierung mit der Pythonliste.

19.7 Glossar