Kapitel 10

Rohübersetzung -- bitte um Rückmeldungen über Fehler und Unklarheiten an glingl@aon.at

Der Datentyp Dictionary

Die zusammengesetzten Datentypen, die wir bisher behandelt haben     Strings, Listen und Tupel     verwenden Ganzzahlen als Indizes. Versucht man, einen anderen Datentyp als Index zu benutzen, erhält man eine Fehlermeldung.

Der Datentyp Dictionary (deutscher Begriff: assoziative Liste, nicht sehr gebräuchlich) ist den anderen zusammengesetzten Datentypen ähnlich. Ein Unterschied besteht darin, dass man beliebige unveränderbare Datentypen für die Indizes verwenden kann. Als Beispiel werden wir ein Dictionary erzeugen um deutsche Wörter in englische Wörter zu übersetzen. Für dieses Dictionary sind die Indizes strings.

Ein Möglichkeit, ein dictionary zu erzeugen, ist mit einem leeren Dictionary zu beginnen und dann Elemente hinzuzufügen.

>>> ger2eng = {}
>>> ger2eng['eins'] = 'one'
>>> ger2eng['zwei'] = 'two'

Die erste Wertzuweisung erzeugt ein Dictionary namens ger2eng; die anderen Wertzuweisungen fügen dem Dictionary weitere Elemente hinzu. Wir können den aktuellen Wert des Dictionary auf die übliche Weise ausgeben:

>>> print ger2eng
{'eins': 'one', 'zwei': 'two'}

Die Elemente des Dictionary erscheinen in Form einer Komma-separierten Liste. Jedes Element enthält einen Index und einen Wert, die durch einen Doppelpunkt voneinander getrennt sind. In einem Dictionary nennt man die Indizes Schlüssel und daher die Elemente Schlüssel-Wert Paare.

Ein andere Möglichkeit, ein Dictionary zu erzeugen, ist eine Liste von Schlüssel-Wert Paaren in genau der Syntax anzugeben, die wir in obiger Ausgabe gesehen haben:

>>> ger2eng = {'eins': 'one', 'zwei': 'two', 'drei': 'three'}

Wenn wir nun den Wert von ger2eng neuerlich ausgeben, erleben wir eine Überraschung:

>>> print ger2eng
{'zwei': 'two', 'eins': 'one', 'drei': 'three'}

Die Schlüssel-Wert Paare sind nicht in der eingegebenen Reihenfolge. Zum Glück gibt es keinen Grund, sich um diese Reihenfolge überhaupt zu kümmern, da die Elemente dieses Dictionary niemals mit ganzen Zahlen indiziert werden. Wir benützen ja statt dessen die Schlüssel um die entsprechenden Werte zu ermitteln:

>>> print ger2eng['zwei']
'two'

Der Schlüssel 'zwei' ergibt den Wert 'two' obwohl er im ersten Schlüssel-Wert Paar erscheint.

10.1 Dictionary Operationen

Die del Anweisung entfernt ein Schlüssel-Wert Paar aus dem Dictionary. Zum Beispiel enthält das folgende Dictionary die Namen verschiedener Früchte und die Angabe, wieviele Früchte jeder Art auf Lager sind:

>>> inventar = {'Aepfel': 430, 'Bananen': 312, 'Birnen': 217, 'Orangen': 525}
>>> print inventar
{'Aepfel': 430, 'Birnen': 217, 'Orangen': 525, 'Bananen': 312}

Wenn jemand alle Birnen kauft, können wir den Eintrag für die Birnen aus dem Dictionary entfernen:

>>> del inventa['Birnen']
>>> print inventar
{'Aepfel': 430, 'Orangen': 525, 'Bananen': 312}

Oder, wenn wir annehmen, dass bald wieder Birnen kommen, können wir den Wert, der mit den Birnen assoziiert ist, ändern:

>>> inventar['Birnen'] = 0
>>> print inventar
{'Aepfel': 430, 'Bananen': 312, 'Orangen': 525, 'Birnen': 0}

Die len Funktion funktioniert auch mit dem Typ Dictionary; sie gibt die Anzahl der Schlüssel-Wert Paare zurück.

>>> len(inventar)
4

10.2 Dictionary Methoden

Eine Methode ist ähnlich einer Funktion     sie übernimmt Parameter und gibt einen Wert zurück     aber die Syntax ist anders. Die keys Methode übernimmt z. B. ein Dictionary und gibt eine Liste von Schlüsseln zurück, die im Dictionary vorkommen. Aber anstatt der Syntax für Funktionen keys(ger2eng) verwenden wir die Methoden-Syntax ger2eng.keys().

>>> ger2eng.keys()
['zwei', 'eins', 'drei']

Diese Form, die sogenannte Punkt Notation gibt den Namen der Funktion, keys, und den Namen des Objekts, auf das die Funktion angewendet wird an, ger2eng. Die runden Klammern zeigen an, dass die Methode keine Parameter übernimmt.

Wir sagen in diesem Fall: wir rufen die Methode keys für das Objekt ger2eng auf.

Die values Methode ist ähnlich; sie gibt eine Liste der Werte in dem Dictionary zurück:

>>> ger2eng.values()
['two', 'one', 'three']

Die items Methode gibt beide zurück, und zwar in der Form eine Liste von Tupeln     eines für jedes Schlüssel-Wert Paar:

>>> ger2eng.items()
[('zwei', 'two'), ('eins', 'one'), ('drei', 'three')]

Die Syntax liefert nützliche Information über die Typen: Die eckigen Klammern zeigen, dass das eine Liste ist. Die runden Klammern zeigen, dass die Elemente der Liste Tupel sind.

Wenn eine Methode ein Argument übernimmt, wird dieselbe Syntax wie für einen Funktionsaufruf verwendet: Zum Beispiel übernimmt die Methode has_key einen Schlüssel als Argument und gibt wahr (1) zurück, falls der Schlüssel im Dictionary vorkommt:

>>> ger2eng.has_key('eins')
1
>>> ger2eng.has_key('due')
0

Versucht man eine Methode ohne das Objekt, zu dem sie gehört, aufzurufen, erhält man eine Fehlermeldung. In diesem Fall ist die Fehlermeldung nicht sehr hilfreich:

>>> has_key('eins')
NameError: has_key

10.3 Aliasnamen and Kopien

Weil der Datentyp Dictionary veränderbar ist, muss man auf Aliasnamen achten. Immer, wenn zwei Variablen auf dasselbe Objekt verweisen betreffen Änderungen der einen auch die andere.

Wenn man ein Dictionary ändern will und eine Kopie des Originals aufbewahren will, muss man die copy - Methode verwenden. Zum Beispiel ist opposites ein Dictionary, das Paare von Gegensätzen enthält:

>>> opposites = {'up': 'down', 'right': 'wrong', 'true': 'false'}
>>> alias = opposites
>>> copy = opposites.copy()

alias und opposites verweisen auf dasselbe Objekt; copy verweist auf eine neue Kopie desselben Dictionary. Wenn man nun alias verändert, wird opposites auch geändert:

>>> alias['right'] = 'left'
>>> opposites['right']
'left'

Wenn wir dagegen copy verändern, bleibt opposites ungeändert:

>>> copy['right'] = 'privilege'
>>> opposites['right']
'left'

10.4 Dünnbesetzte Matrizen

In Abschnitt , haben wir eine Liste von Listen benützt, um Matrizen darzustellen. Das ist eine gute Wahl für Matrizen, bei denen die meisten Elemente ungleich null sind. Betrachten wir nun aber eine Matrix wie die folgende:

Die Listendarstellung enthält eine Menge Nullen:

matrix = [ [0,0,0,1,0],
           [0,0,0,0,0],
           [0,2,0,0,0],
           [0,0,0,0,0],
           [0,0,0,3,0] ]

Eine Alternative dazu ist eine Darstellung mit einem Dictionary: als Schlüssel können wir Tupel verwenden, die die Zeilen- und Spaltenindizes enthalten. Hier ist die Dictionary-Darstellung derselben Matrix:

matrix = {(0,3): 1, (2, 1): 2, (4, 3): 3}

Wir brauchen nur drei Schlüssel-Wert Paare, eines für jedes Element der Matrix, das ungleich null ist. Jeder Schlüssel ist ein Tupel und jeder Wert ist eine Ganzzahl.

Um auf ein Element der Matrix zuzugreifen, könnten wir den [] Operator verwenden:

matrix[0,3]
1

Man beachte, dass die Syntax dafür bei der Dictionary-Darstellung anders ist als bei der Listen-Darstellung. Anstatt zweier Ganzzahl-Indizes benutzen wir nun nur einen Index, und der ist ein Tupel von Ganzzahlen.

Wenn wir ein Element angeben wollen, das null ist, erhalten wir eine Fehlermeldung, weil für den zugehörigen Schlüssel kein Eintrag in dem Dictionary vorhanden ist:

>>> matrix[1,3]
KeyError: (1, 3)

Die get-Methode löst dieses Problem:

>>> matrix.get((0,3), 0)
1

Das erste Argument ist der Schlüssel; das zweite Argument ist der Wert, den get zurückgeben soll, falls der Schlüssel im Dictionary nicht vorkommt:

>>> matrix.get((1,3), 0)
0

get verbessert definitiv den Elemetzugriff auf dünnbesetzte Matrizen. Shame about the syntax.

10.5 Hinweise

Wer ein bisschen mit der fibonacci - Funktion aus Abschnitt 5.7 herumgespielt hat, wird vielleicht bemerkt haben, dass die Funktion umso mehr Rechenzeit braucht, je größer das Argument ist, das man ihr übergibt. Außerdem steigt die Laufzeit außerordentlich schnell an. Auf einer unserer Maschinen ist fibonacci(20) praktisch augenblicklich fertig, fibonacci(30) braucht etwa eine Sekunde und fibonacci(40) braucht grob gesprochen ewig.

Um zu verstehen, warum das so ist, betrachte folgendes Aufruf-Diagramm für fibonacci mit n=4:

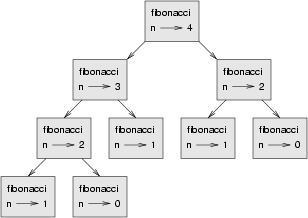
Ein Aufrufdiagram zeigt eine Menge von Funktions-Rahmen, wobei jeder durch Linien mit den Rahmen der Funktionen verbunden ist, die er aufruft. An der Spitze des Diagramms ruft fibonacci mit n=4 fibonacci mit n=3 und n=2 auf. Gleicherweise ruft fibonacci mit n=3 fibonacci mit n=2 und n=1. Und so weiter.

Wenn man abzählt, wie oft fibonacci(0) und fibonacci(1) aufgerufen wurde, bemerkt man, dass dies eine sehr ineffiziente Lösung des Problems ist, und sie wird weit schlimmer, wenn die Argumente noch größer werden.

A good solution is to keep track of values that have already been computed by storing them in a dictionary. A previously computed value that is stored for later use is called a hint. Here is an implementation of fibonacci using hints: Eine gute Lösung dieses Problems wird sein, sich die Werte zu merken, die bereits berechnet worden sind, etwa, indem man sie in einem Dictionary speichert. Ein früher berechneter Wert, der für späteren Gebrauch gespeichert wird, wird ein Hinweis genannt. Hier ist eine Implementation von fibonacci mit Verwendung von Hinweisen.

previous = {0:1, 1:1}

def fibonacci(n):
  if previous.has_key(n):
    return previous[n]
  else:
    newValue = fibonacci(n-1) + fibonacci(n-2)
    previous[n] = newValue
    return newValue

Das Dictionary namens previous speichert die Fibonacci-Zahlen, die wir bereits kennen. Wir beginnen mit nur zwei Paaren: Schlüssel 0 erhält den Wert 1; und Schlüssel 1 erhält den Wert 1.

Wann immer fibonacci aufgerufen wird, überprüft es, ob das Dictionary das Ergebnis schon enthält. Wenn das der Fall ist, wird es sofort zurückgegeben, ohne weitere rekursive Aufrufe auszuführen. Wenn nicht, muss der neue Wert berechnet werden. Er wird dann gleich dem Dictionary hinzugefügt, bevor er von der Funktion zurückgegeben wird.

Mit dieser Version von fibonacci, können unsere Maschinen fibonacci(40) während eines Lidschlags berechnen. Versuchet man aber fibonacci(50) zu berechnen, bekommt man ein anderes Problem:

>>> fibonacci(50)
OverflowError: integer addition

Das Ergebnis ist, wie man gleich sehen wird, 20,365,011,074. Das Problem besteht darin, dass diese Zahl zu groß ist um in eine Python-Ganzzahl, int, hineinzupassen. Zum Glück hat dieses Problem eine leichte Lösung:

10.6 Lange Ganzzahlen

Python stellt einen Datentyp lange Ganzzahl, long int, zur Verfügung, der Ganzzahlen beliebiger Länge speichern und manipulieren kann. Es gibt zwei Möglichkeiten, um einen long int Wert zu erzeugen. Eine ist, eine Ganzzahl hinzuschreiben und dahinter gleich ein großes L anzufügen:

>>> type(1L)
<type 'long int'>

Die andere Möglichkeit ist, die Funktion long zu benutzen, um einen Wert in den Typ long int zu konvertieren. long akzeptiert als Argument jeden numerischen Typ und auch strings, die nur aus Ziffern bestehen.

>>> long(1)
1L
>>> long(3.9)
3L
>>> long('57')
57L

Alle Rechenoperationen funktionieren auch mit long ints, daher haben wir nicht viel zu tun, um fibonacci anzupassen:

>>> previous = {0:1L, 1:1L}
>>> fibonacci(50)
20365011074L

Indem wir gerade einmal die anfänglichen Inhalte von previous geändert haben, haben wir das ganze Verhalten von fibonacci geändert. Die ersten beiden Zahlen in der Folge sind nun long ints, und damit werden es alle anderen Zahlen in dieser Folge auch.

Übung: Ändere factorial so ab, dass es ein das Ergebnis vom Typ long int berechnet.

10.7 Buchstaben zählen

Im Kapitel 7 haben wir eine Funktion geschrieben, die die Anzahl des Auftretens eines Buchstabens in einem String abgezält hat. Eine allgemeinere Version dieses Problems ist, ein Histogramm von Buchstaben in einem String zu erstellen, d. h. festzusztellen, wie oft jeder Buchstabe vorkommt.

Ein solches Histogramm kann etwa dazu benützt werden, um eine Textdatei zu komprimieren. Da verschiedene Buchstaben mit verschiedenen Häufigkeiten auftreten, kann man eine Textdatei komprimieren, indem man kürzere Codes für häufigere Buchstaben einsetzt und längere Codes für Buchstaben, die weniger häufig vorkommen.

Der Datentyp Dictionary ermöglicht Histogramme auf elegante Weise zu erzeugen:

>>> letterCounts = {}
>>> for letter in "Mississippi":
...   letterCounts[letter] = letterCounts.get (letter, 0) + 1
...
>>> letterCounts
{'M': 1, 's': 4, 'p': 2, 'i': 4}

Man beginnt mit einem leeren Dictionary. Für jeden Buchstaben im String finden wir die aktuelle Häufigkeit (eventuell 0) und inkrementieren sie. Am Ende enthält das Dictionary Paare von Buchstaben und ihren Häufigkeiten.

Es mag ansprechender ausschauen, das Histogramm in alphabetischer Reihenfolge auszugeben. Wir können das mit den items und sort Methoden erreichen:

>>> letterItems = letterCounts.items()
>>> letterItems.sort()
>>> print letterItems
[('M', 1), ('i', 4), ('p', 2), ('s', 4)]

Wir haben ja die items Methode schon früher gesehen, aber sort ist die erste Methode für Listen, der wir begegnen. Es gibt noch einige andere Methoden für Listen, darunter append, extend, und reverse. Details kann man der Python-Dokumentation entnehmen.

10.8 Glossar