Kapitel 17

Rohübersetzung -- bitte um Rückmeldungen über Fehler und Unklarheiten an Mike Müller

Verkettete Listen

17.1 Eingeschlossene Verweise

Wir haben Beispiele für Attribute gesehen, die sich auf andere Objekte beziehen. Diese nennt man eingeschlossene Verweise (siehe Abschnitt ). Eine gebräuchliche Datenstruktur, die verkettete Liste, nutzt diese Eigenschaft.

Verkettete Listen bestehen aus Knoten, wobei jeder Knoten einen Verweis zum nächtsen Knoten der Liste enthält. Weiterhin enthält jeder Knoten eine bestimmte Menge Daten, die als Inhalt bezeichnet werden.

Eine verkettete Liste wird als rekursive Datenstruktur betrachtet, weil sie rekursiv definiert ist.

Eine Liste ist entweder:

• eine leere Liste, repräsentiert durch None, oder
• ein Knoten, der ein Objekt als Inhalt und einen Verweis zu einer verkettete Liste enthält.

Für rekursive Datenstrukturen bieten sich rekursive Methoden an.

17.2 Die Klasse Knoten

Wie üblich beim Schreiben einer neuen Klasse beginnen wir mit der Intialisierung und der Methode __str__, damit wir die grundlegenden Mechanismen des Erstellens und Anzeigens eines neuen Datentyps testen können:

class Knoten:
  def __init__(self, inhalt=None, naechster=None):
    self.inhalt = inhalt
    self.naechster  = naechster

  def __str__(self):
    return str(self.inhalt)

Wie gewöhnlich sind die Parameter bei der Initialisierung optional. Ausgangswerte für Inhalt und die Verbindung, nächster, sind None.

Die Textrepräsentation eines Knotens entspricht einfach der Textrepräsentation des Inhalts. Da jeder beliebige Wert an die Funktion str weitergeben werden kann, können wir auch jeden Wert in der Liste speichern.

Um die Implementierung bis zu diesem Punkt zu testen, erstellen wir einen Knoten und drucken ihn aus:

>>> knoten = Knoten("Test")
>>> print knoten
Test

Um die Sache interessanter zu machen, brauchen wir eine Liste mit mehr als einem Knoten:

>>> knoten1 = Konten(1)
>>> knoten2 = Konten(2)
>>> knoten3 = Konten(3)

Es werden drei Knoten erzeugt. Aber wir haben noch keine Liste, da die Knoten noch nicht verkettetet sind. Das Zustandsdiagramm sieht so aus:

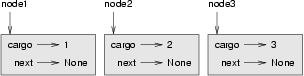
Um die Knoten zu verbinden, müssen wir den ersten Knoten dazu bringen, auf den zweiten zu verweisen. Der zweite muss wiederum auf den dritten Knoten verweisen:

>>> knoten1.naechster = knoten2
>>> knoten2.naechster = knoten3

Der Verweis auf den dritten Knoten ist None, was anzeigt, dass es sich um das Ende der Liste handelt. Jetzt sieht das Zustandsdiagramm so aus:

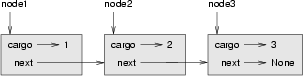
Jetzt weißt du wie man Knoten erstellt und diese zu einer Liste verkettet. Bisher ist aber noch nicht richtig klar geworden warum wir dies tun.

17.3 Listen als Sammlungen

Listen sind nützlich, weil sie eine Möglichkeit darstellen, mehrere Objekte zu einer Einheit zusammenzufassen, die manchmal Sammlung genannt wird. Im Beispiel dient der erste Knoten als Verweis für die gesamte Liste.

Um die Liste als Parameter weiterzugeben, müssen wir nur einen Verweis auf auf den ersten Knoten weitergegeben. Zum Beispiel nimmt die Funktion druckeListe einen einzigen Knoten als Argument. Beginnend vom Kopf der Liste wird jeder Knoten gedruckt, bis das Ende der Liste erreicht ist:

def druckeListe(knoten):
  while knoten:
    print knoten,
    knoten = knoten.naechster
  print

Um diese Methode aufzurufen, geben wir ihr einen Verweis zum ersten Knoten mit:

>>> druckeListe(knoten1)
1 2 3

Innerhalb von druckeListe haben wir einen Verweis auf den ersten Knoten der Liste, aber es gibt keine Variable, die auf die Anderen Knoten verweist. Wir müssen den Wert naechster von jedem Knoten nutzen, um zum nächsten Knoten zu kommen.

Es ist üblich eine Schleifenvariable wie knoten zu nutzen um hintereinander von einem Knoten zum andern zu verweisen und auf diese Weise eine verkettete Liste zu durchlaufen.

Dieses Diagramm zeigt die Knoten in der Liste und die Werte, die die Variable knoten annimmt:

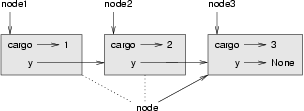
Es ist gebräuchlich, Listen mit eckigen Klammern und mit Kommata zwischen den Elementen zu drucken, also beispielsweise [1, 2, 3]. Ändere bitte druckeListe so ab, das die Liste in diesem Format ausgedruckt wird.

17.4 Listen and Rekursion

Viele Listenoperationen bieten sich für die Nutzung rekursiver Methoden an. Dies verdeutlicht der folgende rekursive Algorithmus zum Rückwärtsdrucken einer Liste:

1. Teile die Liste in zwei Teile: den ersten Knoten (den Kopf); und den Rest (den Schwanz).
2. Drucke den Schwanz rückwärts.
3. Drucke den Kopf.

Natürlich setzt der zweite Schritt, der rekursive Aufruf, voraus, dass wir eine Möglichkeit haben die Liste rückwärts zu drucken. Aber wenn wir annehmen, dass der rekursive Aufruf funktioniert     Vertrauensvorschuss     , können wir uns davon überzeugen, dass dieser Algorithmus funktioniert.

Wir brauchen nun nur einen Basis-Fall und einen Weg, der für jede beliebige Liste garantiert, das dieser auch erreicht wird. Ausgehend von der rekursiven Definition einer Liste bietet sich als Basis-Fall eine leere Liste dargestellt durch None an:

def druckeRueckwaerts(liste):
  if liste == None: return
  kopf = liste
  schwanz = liste.naechste
  druckeRueckwaerts(schwanz)
  print kopf,

Die erste Zeile fängt den Basis-Fall ab, indem sie nichts tut. Die nächsten beiden Zeilen teilen die Liste in kopf und schwanz. Die letzten beiden Zeilen drucken die Liste aus. Das Komma am Ende der letzten Zeile hält Python davon ab nach jedem Knoten eine neue Zeile zu beginnen.

Wir rufen diese Methode genauso auf wie druckeListe:

>>> druckeRueckwaerts(knoten1)
3 2 1

Das Ergebnis ist die Liste in umgekehrter Reihenfolge.

Vielleicht fragst du dich warum druckeListe und druckeRueckwaerts Funktionen und keine Methoden der Klasse Knoten sind. Der Grund liegt darin, dass wir None verwenden, um die leere Liste zu repräsentieren und es nicht erlaubt ist Methoden von None aufzurufen. Diese Einschränkung macht das Schreiben einer sauberen objektorientierten Listenverarbeitung umständlich.

Können wir beweisen, dass druckeRueckwaerts immer zu einem Ende kommt? In anderen Worten, erreicht die Methode immer den Basis-Fall? In der Tat ist die Antwort nein. Bestimmte Arten von Listen bringen sie zum Absturz.

17.5 Unendliche Listen

Es gibt nichts, was einen Knoten davon abhalten würde auf einen früheren Knoten zrückzuverweisen, einschließlich sich selbst. Diese Abbildung zeigt ein Beispiel dafür: eine Liste mit zwei Knoten, von den einer auf sich selbst verweist:

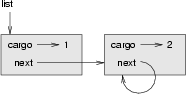
Wenn wir druckeListe mit dieser Liste aufrufen, sind wir in einer unendlichen Schleife gefangen. Wenn wir druckeRueckwaerts aufrufen kommen wir in eine unendliche Rekursion. Dieses Verhalten erschwert das Arbeiten mit unendlichen Listen.

Wie dem auch sei, sie sind gelegentlich nützlich. So können wir z.B. eine Zahl als Liste von Ziffern darstellen und eine unendliche Liste verwenden, um eine sich wiederholende Zahlenfolge abzubilden.

Ungeachtet dessen ist es problematisch, dass wir nicht beweisen können, das druckeListe und druckeRueckwaerts immer zu einem Ende kommen. Wir können bestenfalls die hypothetische Aussage "Wenn die Liste keine Schleifen enthält, dann werden diese Methoden zu einem Ende kommen." machen. Diese Art von Behauptung nennt man eine Vorbedingung. Sie stellt eine Einschränkung für einen der Parameter dar und beschreibt das Verhalten der Methode, wenn diese Einschränkung eingehalten wird. Du wirst bald mehr Beispiele dazu sehen.

17.6 Das grundlegende Theorem der Mehrdeutigkeit

Du bist vielleicht über einen Teil der Funktion druckeRueckwaerts gestoplert:

    kopf = liste
    schwanz = liste.naechste

Nach der ersten Zuweisung haben kopf und liste den gleichen Typ und den gleichen Wert. Warum haben wir dann eine neue Variable definiert?

Der Grund liegt darin, dass die beiden Variablen unterschiedliche Rollen spielen. Wir können uns kopf als Verweis auf einen einzelnen Knoten und liste als Verweis auf den ersten Knoten der Liste vorstellen. Diese "Rollen" sind nicht Teil des Programms sondern existieren nur in der Vorstellung des Programmierers.

Im Allgemeinen können wir aus dem bloßen Betrachten eines Programms nicht ableiten, welche Rolle eine Variable spielt. Diese Mehrdeutigkeit kann nützlich sein. Sie kann aber gleichzeitig ein Programm schwer lesbar machen. Wir verwenden Variablennamen knoten und liste, um zu dokumentieren, wie wir die Varibale verwenden. Manchmal definieren wir zusätzliche Variablen, um Mehrdeutigkeiten zur vermeiden.

Wir hätten druckeRueckwaerts ohne kopf und schwanz schreiben können. Dadurch wäre die Funktion kürzer aber aber möglicherweise auch schlechter verständlich geworden:

def druckeRueckwaerts(liste) :
  if liste == None : return
  druckeRueckwaerts(liste.naechster)
  print liste,

Wenn wir uns die beiden Funktionsaufrufe ansehen, müssen wir wissen, dass druckeRueckwaerts seine Argumente als Sammlung und print sein Argument als einzelnes Objekt behandelt.

Das grundlegende Theorem der Mehrdeutigkeit beschreibt die Mehrdeutigkeit, die einem Verweis auf einen Knoten innewohnt:

Eine Variable, die auf einen Knoten verweist, kann den Knoten entweder als einzelnes Objekt oder als ersten Knoten in einer Liste von Knoten behandeln.

17.7 Listen modifizieren

Es gibt zwei Arten eine verkettete Liste zu modifizieren. Offensichtlich können wir den Ladung eines Knoten ändern, aber die interessanteren Operationen sind die zum Hinzufügen, Entfernen oder Umsortieren von Knoten.

Als Beispiel schreiben wir eine Methode, die den zweiten Knoten der Liste entfernt und einen Verweis zum entfernten Knoten liefert:

def entferneZweiten(liste):
  if liste == None: return
  erster = liste
  zweiter = liste.naechster
  # lasse den ersten Knoten auf den dritten verweisen
  erster.naechster = zweiter.naechster
  # trenne den zweiten Knoten vom Rest der Liste
  zweiter.naechster = None
  return zweiter

Wir nutzen wieder eine temporäre Variable, um den Code lesbarer zu machen. So wird diese Methode verwendet:

>>> druckeListe(knoten1)
1 2 3
>>> entfernt = entferneZweiten(knoten1)
>>> druckeListeList(entfernt)
2
>>> druckeListe(knoten1)
1 3

Dieses Zustandsdiagramm zeigt den Effekt dieser Operation:

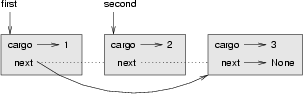
Was passiert, wen du diese Methode aufrufst und ihr eine Liste mit nur einem Element, einem so genannten Singelton übergibst? Was passiert, wenn du eine leere Liste als Argument mitgibst? Gibt es eine Vorbedingung für die Methode? Wenn ja, ändere die Methode so, dass sie eine Verletzung dieser Vorbedingung auf sinnvolle Weise behandelt.

17.8 Hüllen und Helfer

Es ist ist nützlich eine Listenoperation auf zwei Methoden aufzuteilen. Zum Beispiel können wir, um eine Liste im normalen Format rückwärts zu drucken [3, 2, 1], die druckeRueckwaerts-Methode verwenden. Da das Ergebnis so 3,
2, aussieht, benötigen wir aber noch eine weitere Methode, um die Klammern und den ersten Knoten zu drucken. Nennen wir diese Methoden druckeRueckwaertsHuebsch:

def druckeRueckwaertsHuebsch(liste) :
  print "[",
  if liste != None :
    kopf = liste
    schwanz = liste.naechster
    druckeRueckwaerts(schwanz)
    print kopf,
  print "]",

Wieder ist es eine gute Idee Methoden wie diese zu kontrollieren, um herauszufinden, ob sie mit Spezialfällen wie leeren Listen or Singeltons umgehen können.

Wenn wir diese Methode an einer anderen Stelle im Programm verwenden, rufen wir die Methode druckeRueckwaertsHuebsch direkt, die wiederum die Method druckeRueckwaerts in unserem Auftrag ruft. In diesem Sinne handelt druckeRueckwaertsHuebsch wie eine Hülle, die druckeRueckwaerts als Helfer nutzt.

17.9 Die Klasse VerketteteListe

Mit der Art der Implementierung der Liste sind einige Probleme verbunden, die nicht gleich offensichtlich sind. In Umkehrung von von Ursache und Wirkung werden wir zuerst eine alternative Implementierung vorschlagen und dann das Problem erläutern.

Zuerst definieren wir eine neue Klasse VerketteteListe. Ihre Attribute sind eine Ganzzahl, die die Länge der Liste enthält und ein Verweis auf den ersten Knoten. Objekte der Klasse VerketteteListe dienen als Zugriffspunkte zum Verändern der Listen mit Knoten-Objekten:

class VerketteteListe :
  def __init__(self) :
    self.laenge = 0
    self.kopf   = None

Die VerketteteListe hat eine angenehme Eigenschaft, denn sie bietet einen natürlichen Platz für Hüllfunktionen wie druckeRueckwaertsHuebsch, die in eine Methode der Klasse VerketteteListe umgewandelt werden können:

class VerketteteListe:
  ...
  def druckeRueckwaertsHuebsch(self):
    print "[",
    if self.kopf != None:
      self.kopf.druckeRueckwaerts()
    print "]",

class Knoten:
  ...
  def druckeRueckwaerts(self):
    if self.naechster != None:
      schwanz = self.naechster
      schwanz.druckeRueckwaerts()
    print self.ladung,

Um die Sache ein wenig zu verwirren haben wir druckeRueckwaertsHuebsch umbenannt. Es gibt jetzt zwei Methoden, die druckeRueckwaerts heißen: eine in der Klasse Knoten (dem Helfer); und eine in der Klasse VerketteteListe (der Hülle). Wenn die Hülle self.kopf.druckeRueckwaerts ruft, wird wiederum der Helfer gerufen, da self.kopf ein Knoten-Objekt ist.

Ein weiter Nutzen der Klasse VerketteteListe liegt darin, dass es einfacher wird das erste Element zu entfernen. Zum Beispiel ist addiereErsten eine Methode für VerketteteListe. Sie nimmt einen Inhalt als Argument und legt es am Beginn der Liste ab:

class VerketteteListe:
  ...
  def addiereErsten(self, inhalt):
    knoten = Knoten(inhalt)
    knoten.naechster = self.kopf
    self.kopf = knoten
    self.laenge = self.laenge + 1

Wie gewöhnlich solltest du Code wie diesen kontrollieren, ob er die Spezialfälle behandelt. Was passiert zum Beispiel wenn die Liste anfangs leer ist?

17.10 Unveränderliche

Manche Listen sind "wohlgeformt"; andere nicht. Zum Beispiel kann eine Liste, die eine Schleife enthält viele unserer Methoden zum Absturz bringen. Eine Anforderung an eine Liste könnte deshalb sein, dass sie keine Schleifen enthalten darf. Eine andere Forderung bestünde darin, dass der Wert für laenge im Objekt VerketteteListe gleich der aktuellen Anzahl von Listenknoten sein soll.

Solcherart Anforderungen werden Unveränderliche genannt, weil sie idealer Weise für alle Objekte und für alle Fälle wahr sein sollten. Die Definition von Unveränderlichen für Objekte ist eine nützliche Programmierpraxis, weil sie die Korrektheitsprüfung von Code vereinfacht, die Integrität von Datenstrukturen kontrolliert und Fehler aufspürt.

Manchmal werden diese Unveränderlichen verletzt, was zu Verwirrung führen kann. So ist zum Beispiel in der Mitte von addiereErsten, nach dem Hinzufügen eines Knotens aber noch vor dem Hochzählen von laenge die Unveränderliche verletzt. Diese Art der Verletzung ist akzeptabel. In der Tat ist es oft unmöglich ein Objekt zu modifizieren, ohne eine Unveränderliche zumindest kurzzeitig zu verletzen. Normalerweise fordern wir, dass jede Methode, die eine Unveränderliche verletzt, diese wieder herstellen muss.

Wenn die Verletzung der Unveränderlich über einen größeren Codebereich geht, ist es wichtig diese durch Kommentare klar zu verdeutlichen, so dass keine Operation ausgeführt wird, die von der Unveränderlichen abhängt.

17.11 Glossary