






 |
 |
 |
 |
 |
 |
 |
Rohübersetzung -- bitte um Rückmeldungen über Fehler und Unklarheiten an glingl@aon.at
Als ein weiteres Beispiel eines benutzerdefinierten Datentyps werden wir eine Klasse Time definieren, die eine Tageszeit Angabe speichern kann. Die Klassendefinition sieht so aus:
class Time:
pass
Nun können wir ein neues Time Objekt erzeugen und Attribute für Stunden, Minuten und Sekunden hinzufügen:
time = Time()
time.hours = 11
time.minutes = 59
time.seconds = 30
Das Zustandsdiagramm, für das Time Objekt sieht so aus:
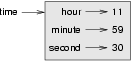
Übung: Schreibe eine Funktion printTime, die ein Time Objekt als Argument übernimmt und die Zeit in der Form hours:minutes:seconds ausruckt.
(Noch eine) Übung: Schreibe eine bool'sche Funtion after, die zwei Time Objekte, t1 und t2, als Argumente übernimmt und die True zurückgibt, wenn t1 chronologisch auf t2 folgt. Andernfalls gibt sie False zurück.
In den nächsten Abschnitten werden wir zwei Versionen einer Funktion schreiben, die wir addTime nennen und die die Summe von zwei Zeiten, Time-Werten, berechnet. Diese beiden Versionen sollen als Beispiele für zwei Arten von Funktionen dienen: reine Funktionen einerseits und modifizierende Funktionen andererseits.
Folgendes ist eine Rohfassung von addTime:
def addTime(t1, t2):
sum = Time()
sum.hours = t1.hours + t2.hours
sum.minutes = t1.minutes + t2.minutes
sum.seconds = t1.seconds + t2.seconds
return sum
Diese Funktion erzeugt ein neues Time Objekt, initialisiert seine Attribute und gibt einen Verweis auf dieses neue Objekt zurück. So etwas nennt man eine reine Funktion, weil sie keines der Objekte, die ihr als Argumente übergeben werden verändert und weil sie keine Seiteneffekte, wie z. B. Ausgabe eines Wertes mit der print-Anweisung oder Einlesen einer Benutzereingabe hat.
Hier ein Beispiel, wie man diese Funktion benutzen kann: Wir erzeugen zwei Time Objekte: currentTime, welches die momentane Zeit enthält und breadTime, welches jenes Zeitmaß enthält, das ein Bäcker braucht, um Brot zu backen. Dann benutzen wir addTime um heraus zu finden, wann das Brot fertig sein wird. Wenn du noch nicht fertig bist mit dem Programmieren von printTime, sieh einmal weiter unten nach im Abschnitt_14.2 , befor du folgendes versuchst:
>>> currentTime = Time()
>>> currentTime.hours = 9
>>> currentTime.minutes = 14
>>> currentTime.seconds = 30
>>> breadTime = Time()
>>> breadTime.hours = 3
>>> breadTime.minutes = 35
>>> breadTime.seconds = 0
>>> doneTime = addTime(currentTime, breadTime)
>>> printTime(doneTime)
Die Ausgabe dieses Programms ist 12:49:30, und das ist korrekt. Andererseits gibt es aber Fälle, bei denen das Ergebnis nicht korrekt ist. Fällt dir ein solcher Fall ein?
Das Problem rührt daher, dass diese Funktion nicht solche Fälle berücksichtigt, wo die Anzahl der Sekunden (oder der Minuten) sich auf über sechzig zusammen addiert. Wenn dies geschieht, haben wir 6o Extra-Sekunden, die wir auf die Minuten "übertragen" müssen, oder (analog) 60 Extra-Minuten auf die Stunden .
Hier ein zweite korrigierte Fassung der Funktion:
def addTime(t1, t2):
sum = Time()
sum.hours = t1.hours + t2.hours
sum.minutes = t1.minutes + t2.minutes
sum.seconds = t1.seconds + t2.seconds
if sum.seconds >= 60:
sum.seconds = sum.seconds - 60
sum.minutes = sum.minutes + 1
if sum.minutes >= 60:
sum.minutes = sum.minutes - 60
sum.hours = sum.hours + 1
return sum
Diese Funktion ist zwar korrekt, der Funktionskörper wird aber schon ziemlich lang. Später werden wir zu einer alternativen Lösung raten, der einen kürzeren Code liefert.
Manchmal ist es nützlich, wenn eine Funktion ein oder mehrere der Objekte verändert, die sie als Argumente übergeben kriegt. Normalerweise behält ja die aufrufende Funktion Verweise auf diese Objekte, sodass jede Veränderung dieser Objekte in der aufrufenden Funktion sichtbar sind. Funktionen, die auf diese Weise arbeiten, nennen wir modifizierende Funktionen.
Eine Funktion increment, die zu einem Time-Objekt eine gegebene Anzahl von Sekunden addiert, kann in natürlicher Weise als eine modifizierende Funktion geschrieben werden. Ein grober Entwurf dieser Funktion sieht so aus:
def increment(time, seconds):
time.seconds = time.seconds + seconds
if time.seconds >= 60:
time.seconds = time.seconds - 60
time.minutes = time.minutes + 1
if time.minutes >= 60:
time.minutes = time.minutes - 60
time.hours = time.hours + 1
Die erste Zeile führt die grundlegende Rechenoperation aus, der Rest sorgt für die Behandlung der Spezialfälle, wie wir schon oben gesehen haben.
Ist diese Funktion korrekt? Was geschieht, wenn der Parameter secs viel größer als sechzig ist? In diesem Fall reicht ein Übertrag von 1 nicht, sondern wir müssen so oft 60 Sekunden als eine Minute übertragen, bis seconds kleiner als sechzig ist. Eine Lösung dafür ist, die if Anweisungen durch while Anweisungen zu ersetzen:
def increment(time, secs):
time.seconds = time.seconds + secs
while time.seconds >= 60:
time.seconds = time.seconds - 60
time.minutes = time.minutes + 1
while time.minutes >= 60:
time.minutes = time.minutes - 60
time.hours = time.hours + 1
Diese Funktion ist nun korrekt, aber es ist nicht die effizienteste Lösung.
Übung: Schreibe diese Funktion neu, so dass sie keine Schleifen mehr enthält.
(Noch eine) Übung: Schreibe increment als reine Funktion, und schreibe dann auch Funktionsaufrufe für beide Fassungen.
Alles, was mit modifizierenden Funktionen gemacht werden kann, kann auch mit reinen Funktionen gemacht werden. In der Tat gibt es sogar einige Programmiersprachen, die nur reine Funktionen gestatten. Einiges spricht dafür, dass Programme, die nur reine Funktionen verwenden, schneller entwickelt werden können und weniger fehleranfällig sind, als Programme, die modifizierende Funktionen verwenden. Nichtsdestoweniger sind modifizierende Funktionen manchmal sehr praktisch. Auch sind in manchen Fällen funktionale Programme weniger effizient.
Wir empfehlen im allgemeinen, reine Funktione zu schreiben, wann immer es vernünftig erscheint. Zu modifizierenden Funktionen sollte man nur greifen, wenn es einen überzeugenden Vorteil bringt. Diesen Zugang könnte man auch einen funktionalen Programmierstil nennen.
In diesem Kapitel haben wir einen Zugang zur Programmentwicklung vorgeführt, den man Prototyp Entwicklung nennt. Wir haben in jedem Fall einen rohen Entwurf (oder Prototyp) erstellt, der die grundlegenden Berechnungen ausgeführt hat und ihn dann mit einigen speziellen Daten getestet. Dabei haben wir Schwächen und Fehler gefunden und korrigiert.
Dieser Zugang ist zwar effektiv, er kann aber zu Code führen, der unnötig kompliziert ist -- weil er viele Spezialfällen behandelt -- und unzuverlässig ist -- weil es schwer möglich ist, zu beurteilen ob man alle Fehler gefunden hat.
Eine Alternative dazu ist geplante Entwicklung. Für sie muss man sich zunächst ein weitgehendes Verständnis des Problems erarbeiten. Dafür wird dann das Programmieren viel leichter. In unserem Beispiel besteht dieses Verständnis z. B. in der Einsicht, dass ein Time Objekt in Wirklichkeit eine dreistellige Zahl im Stellenwertsystem mit der Basis 60 ist. second, die Sekunden-Komponente ist die "Einer-Stelle", minute, die Minuten-Komponente ist die "Sechziger-Stelle" und hour, die Stunden-Komponente, ist die "Dreitausendsechshunderter-Stelle".
Wie wir addTime und increment geschreiben haben, haben wir in der Tat Additionen mit der Basis 60 ausgeführt, weshalb wir diese Überträge von einer zur nächsten Stelle gebraucht haben.
Diese Beobachtung legt einen anderen Zugang zu dem ganzen Problem nahe wir
können ein Time Objekt in eine einzige Zahl umwandeln und einen
Vorteil aus dem Umstand ziehen, dass der Computer ja weiß, wie man mit
Zahlen rechnet. Die folgende Funktion wandelt ein Time-Objekt in
eine ganze Zahl um:
def convertToSeconds(t):
minutes = t.hours * 60 + t.minutes
seconds = minutes * 60 + t.seconds
return seconds
Jetzt brauchen wir nur noch die Möglichkeit, eine ganze Zahl in ein Time Objekt umzuwandeln:
def makeTime(secs):
time = Time()
time.hours = secs/3600
secs = secs - time.hours * 3600
time.minutes = secs/60
secs = secs - time.minutes * 60
time.seconds = secs
return time
Wahrscheinlich musst du ein wenig nachdenken, um dich davon zu überzeugen, dass diese Technik der Umwandlung von einer Basis in eine andere Basis korrekt ist. Nehmen wir aber einmal an, du bis davon überzeugt, dann kannst du nun diese Funktion dazu benützen, um auch noch die addTime umzuschreiben:
def addTime(t1, t2):
seconds = convertToSeconds(t1) + convertToSeconds(t2)
return makeTime(seconds)
Diese Version ist viel kürzer als die ursprüngliche, und es ist auch viel leichter zu zeigen, dass sie korrekt ist (wie gewohnt unter der Annahme, dass die Funktionen, die sie aufruft, korrekt sind.)
Übung: schreibe increment auf die selbe Weie um.
In einem gewissen Sinn ist dieses Umwandeln von Basis 60 nach Basis 10 und wieder zurück schwieriger, als einfach mit Zeitangaben zu operieren. Basis-Umwandlung ist abstrakter; unsere Inuition für den Umgang mit Zeiten ist besser.
Wenn wir aber die Einsicht haben, dass Zeitangaben als Basis-60-Zahlen behandelt werden können, und wenn wir uns für die Investition entscheiden, diese Umwandlungsfunktionen (convertToSeconds und makeTime) zu schreiben, dann bekommen wir ein kürzeres, leichter lesbares Programm, das überdies leichter von Fehlern zu befreien und zuverlässiger ist.
Zusätzlich ist es auch leichter, später neue Programmerweiterungen hinzuzufügen. Stelle dir z.B. vor, du möchtest die Subtraktion zweier Zeiten implementieren, um die Dauer des Zeitintervalls zwischen ihnen heraus zu finden. Der naive Zugang wäre, diese Subtraktion mit "Ausborgen von der nächsthöheren Stelle" zu implementieren. Mit unseren Umwandlungsfunktionen würde die Sache aber leichter sein und auch mit höherer Wahrscheinlichkeit korrekt.
Witzigerweise ist es manchmal so, das man ein Problem, wenn man es schwieriger (und allgemeiner) angeht, schließlich leichter macht. (Denn es sind dann weniger Spezialfälle zu beachten und weniger Gelegenheiten vorhanden, Fehler zu machen.)
Wenn du eine allgemeine Lösung für eine Klasse von Problemen schreibst, im Gegensatz zu einer speziellen Lösung für ein einzelnes Problem, dann hast du einen Algorithmus geschrieben. Wir haben diesen Begriff schon früher erwähnt, wir haben ihn aber nicht sorgfältig definiert. Er ist nämlich nicht leicht zu definieren. Wir werden daher ein paar Versuche machen:
Zuerst betrachten wir etwas, was kein Algorithmus ist. Wie du gelernt hast, wie man einstellige Zahlen multipliziert, hast du wahrscheinlich einfach die "Multiplikations-Tabelle" auswendig gelernt. Das heißt, du hast einfach 100 spezielle Ergebnisse auswendig gelernt. Diese Art von Wissen ist kein Algorithmus.
Wenn du aber "faul" warst, hast du dabei vielleicht ein wenig getrickst, indem du ein paar Abkürzungen geleernt hast. Um zum Beispiel das Produkt von n und 9 zu finden, kannst du n-1 als die erste Ziffer schreiben und 10-n als die zweite Ziffer. Dieser Trick ist eine allgemeine Lösung für die Multiplikation einer einziffrigen Zahl mit 9. Das ist ein Algorithmus!
In ähnlicher Weise sind die Techniken für das Addieren (mit Übertrag), für das Subtrahieren (mit Ausborgen) und für das Dividieren alle Algorithmen. Eine chrakteristische Eigenschaft von Algorithmen ist, das man keinerlei Intelligenz braucht, um sie auszuführen. Sie sind mechanische Vorgänge, wo jeder Schritt auf den vorigen entsprechend einem einfachen Satz von Regeln folgt.
Unserer Meinung nach ist es erstaunlich, dass die Menschen in der Schule so viel Zeit damit verbringen, zu lernen, wie man Algorithmen ausführt, die, buchstäblich, keine Intelligenz erfordern.
Andererseits ist der Prozess des Entwurfs von Algorithmen durchaus interessant, intellektuell herausfordernd, und durchaus ein zentraler Bestandteil dessen, was wir Programmieren nennen.
Manches von dem, was die Leute ganz selbstverständlich tun, ohne dabei Schwierigkeiten zu haben oder bewusst darüber nachzudenken, gehört zu den Vorgängen, die am Schwierigsten algorithmisch auszudrücken sind. Das Verstehen natürlicher Sprache ist ein gutes Beispiel dafür. Wir alle können das, aber bis heute war niemand in der Lage zu erklären, wie wir das tun, jedenfalls nicht in der Form eines Algorithmus.
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
 |
 |
 |
 |
 |
 |
 |